Diferenças entre edições de "Campo"
| (Há uma edição intermédia do mesmo utilizador que não está a ser apresentada) | |||
| Linha 4: | Linha 4: | ||
*CONTEXTO : Primeiro ciclo universitário | *CONTEXTO : Primeiro ciclo universitário | ||
*AREA: Matemática | *AREA: Matemática | ||
| − | *DISCIPLINA: Calculo | + | *DISCIPLINA: Calculo Diferencial e Integral 2 |
*ANO: 1 | *ANO: 1 | ||
*LINGUA: pt | *LINGUA: pt | ||
| − | *AUTOR: | + | *AUTOR: Ana Moura Santos e Miguel Dziergwa |
| − | *MATERIA PRINCIPAL: | + | *MATERIA PRINCIPAL: Campos gradientes e potenciais escalares |
| − | *DESCRICAO: | + | *DESCRICAO: Identificação gráfica do campo gradiente |
| − | *DIFICULDADE: | + | *DIFICULDADE: ** |
*TEMPO MEDIO DE RESOLUCAO: 15 mn | *TEMPO MEDIO DE RESOLUCAO: 15 mn | ||
| − | *TEMPO MAXIMO DE RESOLUCAO: | + | *TEMPO MAXIMO DE RESOLUCAO: 20 mn |
| − | *PALAVRAS CHAVE: | + | *PALAVRAS CHAVE: campo vetorial, representação gráfica do campo gradiente |
</div> | </div> | ||
</div> | </div> | ||
| Linha 25: | Linha 25: | ||
[[File:CampoRespostas.gif]] | [[File:CampoRespostas.gif]] | ||
| − | A)\(4\) | + | A) \(4\) |
| − | B)\(1\) | + | B) \(1\) |
| − | C)\(2\) | + | C) \(2\) |
| − | D)\(3\) | + | D) \(3\) |
Edição atual desde as 13h42min de 26 de março de 2018
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo Diferencial e Integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Campos gradientes e potenciais escalares
- DESCRICAO: Identificação gráfica do campo gradiente
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 20 mn
- PALAVRAS CHAVE: campo vetorial, representação gráfica do campo gradiente
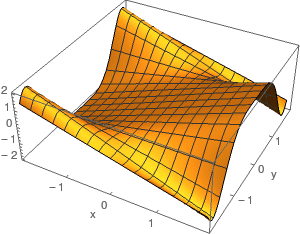
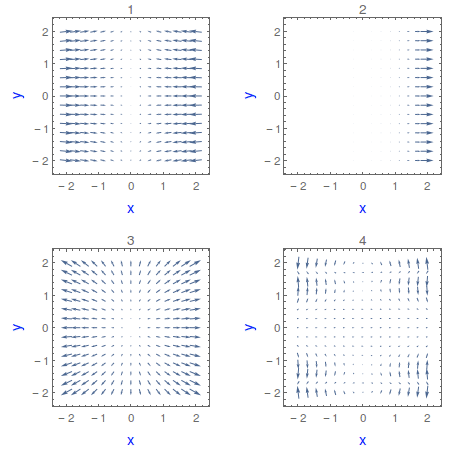
Na figura está representado o gráfico duma função escalar nas variáveis \(x\) e \(y\), para \( -2 \leq x \leq 2\) e \(-2 \leq y \leq 2\).
Sabendo que o comprimento de cada seta com origem no ponto \(\left(\begin{array}{c}x\\y\\\end{array}\right)\) é proporcional à norma do vetor gradiente nesse ponto, indique qual poderá ser a figura que corresponde ao campo gradiente da função, isto é\(\begin{array}{cccc}\text{$\nabla$f:}&\mathbb{R}^2&\to&\mathbb{R}^2\\\text{}&\left(\begin{array}{c}x\\y\\\end{array}\right)&|\rightarrow&\left(\begin{array}{c}\frac{\text{$\partial$f}}{\text{$\partial$x}}\\\frac{\text{$\partial$f}}{\text{$\partial$y}}\\\end{array}\right)\\\end{array}\)
A) \(4\)
B) \(1\)
C) \(2\)
D) \(3\)
Para obter o zip que contém as instâncias deste exercício clique aqui(campo)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt