Diferenças entre edições de "Quadro suspenso"
Saltar para a navegação
Saltar para a pesquisa
| (Há 5 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 17: | Linha 17: | ||
</div> | </div> | ||
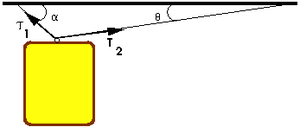
| − | [[File: | + | [[File:MO_quadro_do_tecto_sem_corda.png|thumb|Quadro suspenso]] |
| − | Um quadro está suspenso do tecto como indicado na figura. O quadro pesa \(5\) Kg. | + | Um quadro está suspenso do tecto como indicado na figura. O quadro pesa \(5\) Kg. |
| + | |||
| + | Considere \(g \simeq 9.81\) m.s\(^{-2}\). | ||
* Escolha o sistema de coordenadas para estudar o comportamento do sistema (quadro). | * Escolha o sistema de coordenadas para estudar o comportamento do sistema (quadro). | ||
| Linha 27: | Linha 29: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | + | Um dos sistemas de coordenadas mais indicados, e que será considerado daqui para a frente, é colocar o eixo dos xx na horizontal para a direita e os yy na vertical para cima. | |
</div> | </div> | ||
| Linha 38: | Linha 40: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | \( | + | \( m\frac{d^2x}{dt^2} = -T_1 \cos{\alpha} + T_2 \cos{\theta} \) |
| + | |||
| + | \( m\frac{d^2y}{dt^2} = T_1 \sin{\alpha} + T_2 \sin{\theta} -mg \) | ||
</div> | </div> | ||
</div> | </div> | ||
| − | * Se o quadro estiver parado, calcule a expressão e calcule o valor de \(T_1\). O mesmo para \(T_2\) | + | * Se o quadro estiver parado, calcule a expressão e calcule o valor de \(T_1\). O mesmo para \(T_2\). Considere \(\alpha = 35^º\) e \(\theta = 25^º\). |
<div class="toccolours mw-collapsible mw-collapsed" style="width:260px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:260px"> | ||
| Linha 49: | Linha 53: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | \( | + | * \( T_1 \simeq 51.3 \) N |
| + | |||
| + | * \( T_2 \simeq 46.4 \) N | ||
</div> | </div> | ||
</div> | </div> | ||
Edição atual desde as 00h02min de 28 de outubro de 2015
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Mecânica e ondas
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Mourão
- MATERIA PRINCIPAL: Equilíbrio de Sistemas
- DESCRICAO: Quadro suspenso
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 600 [s]
- TEMPO MAXIMO DE RESOLUCAO: 1200 [s]
- PALAVRAS CHAVE: Tensão, Equilíbrio, Estático, Leis, Newton
Um quadro está suspenso do tecto como indicado na figura. O quadro pesa \(5\) Kg.
Considere \(g \simeq 9.81\) m.s\(^{-2}\).
- Escolha o sistema de coordenadas para estudar o comportamento do sistema (quadro).
Respostas
Um dos sistemas de coordenadas mais indicados, e que será considerado daqui para a frente, é colocar o eixo dos xx na horizontal para a direita e os yy na vertical para cima.
- Escreva a equação de Newton por componentes para o quadro.
Respostas
\( m\frac{d^2x}{dt^2} = -T_1 \cos{\alpha} + T_2 \cos{\theta} \)
\( m\frac{d^2y}{dt^2} = T_1 \sin{\alpha} + T_2 \sin{\theta} -mg \)
- Se o quadro estiver parado, calcule a expressão e calcule o valor de \(T_1\). O mesmo para \(T_2\). Considere \(\alpha = 35^º\) e \(\theta = 25^º\).
Respostas
- \( T_1 \simeq 51.3 \) N
- \( T_2 \simeq 46.4 \) N