Diferenças entre edições de "Notas de apoio às aulas teóricas"
| (Há 22 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 8: | Linha 8: | ||
Exemplos: | Exemplos: | ||
| − | + | <center> | |
| − | + | \begin{array}{rl} | |
| + | f(x, y)=x^3y^2 &\implies \frac{\partial f}{\partial x} = 3x^2y^2, \quad \frac{\partial f}{\partial y} = 2x^3y \\ | ||
| + | f(x, y)=e^{-y}\sin(x) &\implies \frac{\partial f}{\partial x} = e^{-y}\cos(x), \quad \frac{\partial f}{\partial y} = -e^{-y}\sin(x) | ||
| + | \end{array} | ||
| + | </center> | ||
=Resolução de equações diferenciais lineares do primeiro grau= | =Resolução de equações diferenciais lineares do primeiro grau= | ||
Este tipo de equações aparece, por exemplo, em situações em que uma força (tipicamente o atrito) é proporcional à velocidade, tais como a queda de uma gotícula de óleo na [[Experiência de Millikan]]. A equação envolve a primeira derivada, um termo linear e um termo constante, e podemos escrever a seguinte expressão genérica: | Este tipo de equações aparece, por exemplo, em situações em que uma força (tipicamente o atrito) é proporcional à velocidade, tais como a queda de uma gotícula de óleo na [[Experiência de Millikan]]. A equação envolve a primeira derivada, um termo linear e um termo constante, e podemos escrever a seguinte expressão genérica: | ||
| − | <math> | + | <center><math> |
a \frac{df}{dt} = b - cf | a \frac{df}{dt} = b - cf | ||
| − | </math> | + | </math></center> |
| − | em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a, b\) e \(c\) são constantes. | + | em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a, b\) e \(c\) são constantes. Para resolver esta equação, vamos recorrer a uma função auxiliar \(g(t)\) definida como: |
| − | + | <center><math> | |
| − | |||
| − | <math> | ||
g(t) = f(t) - \frac{b}{c} | g(t) = f(t) - \frac{b}{c} | ||
| − | </math> | + | </math></center> |
Se derivarmos esta igualdade verificamos que as derivadas de ambas as funções são iguais: | Se derivarmos esta igualdade verificamos que as derivadas de ambas as funções são iguais: | ||
| − | <math> | + | <center><math> |
\frac{dg}{dt} = \frac{df}{dt} | \frac{dg}{dt} = \frac{df}{dt} | ||
| − | </math> | + | </math></center> |
| − | Inserindo estas duas igualdades na primeira equação, podemos escrevê-la na forma | + | Inserindo estas duas igualdades na primeira equação, podemos escrevê-la na forma |
| − | <math> | + | <center><math> |
a \frac{dg}{dt} = c \left( \frac{b}{c} - f(t) \right) = -cg(t) | a \frac{dg}{dt} = c \left( \frac{b}{c} - f(t) \right) = -cg(t) | ||
| − | |||
| − | |||
| − | |||
\implies \frac{dg}{dt} = -\frac{c}{a} g(t) | \implies \frac{dg}{dt} = -\frac{c}{a} g(t) | ||
| − | </math> | + | </math></center> |
| − | A última igualdade apresenta-nos então a questão: qual a função cuja derivada é igual à própria função, multiplicada por uma constante? Não é difícil concluir que é a função exponencial, mais concretamente: | + | A última igualdade apresenta-nos então a questão: ''qual a função cuja derivada é igual à própria função, multiplicada por uma constante''? Não é difícil concluir que é a função exponencial, mais concretamente: |
| − | <math> | + | <center><math> |
g(t) = A e^{-\frac{c}{a}t} | g(t) = A e^{-\frac{c}{a}t} | ||
| − | </math> | + | </math></center> |
é a solução daquela equação, em que \(A\) é uma constante que é necessário introduzir, e que depende das condições iniciais do sistema. Agora que determinámos a solução para \(g(t)\), podemos calcular a função \(f(t)\) original: | é a solução daquela equação, em que \(A\) é uma constante que é necessário introduzir, e que depende das condições iniciais do sistema. Agora que determinámos a solução para \(g(t)\), podemos calcular a função \(f(t)\) original: | ||
| − | <math> | + | <center><math> |
f(t) = g(t) + \frac{b}{c} = A e^{-\frac{c}{a}t} + \frac{b}{c} | f(t) = g(t) + \frac{b}{c} = A e^{-\frac{c}{a}t} + \frac{b}{c} | ||
| − | </math> | + | </math></center> |
Para determinar o valor de \(A\), temos que ter alguma informação sobre o sistema. Por exemplo, sabendo que o valor inicial da função \(f(t)\) é \(f(0) = f_0\), podemos escrever: | Para determinar o valor de \(A\), temos que ter alguma informação sobre o sistema. Por exemplo, sabendo que o valor inicial da função \(f(t)\) é \(f(0) = f_0\), podemos escrever: | ||
| − | <math> | + | <center><math> |
f(0) \equiv f_0 = A + \frac{b}{c} \implies A = f_0 - \frac{b}{c} | f(0) \equiv f_0 = A + \frac{b}{c} \implies A = f_0 - \frac{b}{c} | ||
| − | </math> | + | </math></center> |
| + | |||
| + | Inserindo esta expressão no valor de \(A\) e simplificando, temos finalmente a solução geral da equação original: | ||
| + | |||
| + | <center><math> | ||
| + | f(t)=f_0e^{-\frac{c}{a}t}+\frac{b}{c}\left(1-e^{-\frac{c}{a}t}\right) | ||
| + | </math></center> | ||
| + | |||
| + | Quando \(t\rightarrow\infty\) a função atinge um valor limite \(f_{lim}=b/c\), independentemente do valor da | ||
| + | velocidade inicial. Podemos ainda definir um “tempo médio” \(\tau=a/c\) para a função exponencial. | ||
| + | |||
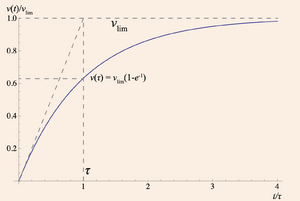
| + | A tabela em baixo mostra a aplicação da resolução acima à Experiência de Millikan. A figura mostra a evolução de uma função \(v(t)\), solução de uma equação deste tipo, e resume a interligação entre todos os parâmetros apresentados. Note que os eixos são normalizados, isto é, os seus valores são divididos por constantes características do problema (neste caso, o tempo médio \(\tau\) e a velocidade limite \(v_{lim}\). | ||
| + | [[file:millikan-graph.png|thumb|upright=1.0 |alt=Evolução da velocidade de um corpo em queda livre sujeito a uma força de atrito. |Fig. 1 - Evolução da velocidade de um corpo em queda livre sujeito a uma força de atrito.]] | ||
| + | |||
| + | {| class="wikitable" style="text-align: center;" | ||
| + | ! !! Exp. Millikan | ||
| + | |- | ||
| + | | Eq. diferencial || \(m \frac{dv}{dt} = mg - knv\) | ||
| + | |- | ||
| + | | Função \(f(t)\) || Velocidade \(v(t)\) | ||
| + | |- | ||
| + | | \(df/dt\) || Aceleração \(a(t) = dv/dt\) | ||
| + | |- | ||
| + | | \(a\) || \(m\) | ||
| + | |- | ||
| + | | \(b\) || \(mg\) | ||
| + | |- | ||
| + | | \(c\) || \(kn\) | ||
| + | |- | ||
| + | | \(A\) || \(f_0 = \text{Vel. inicial} = 0 \, \text{m/s}\) | ||
| + | |- | ||
| + | | Expressão || \(\frac{mg}{kn} \left[ 1 - \exp\left(-\frac{kn}{m}t\right) \right]\) | ||
| + | |- | ||
| + | | \(f_{\text{lim}}\) || \(v_{\text{lim}} = \frac{mg}{kn}\) | ||
| + | |- | ||
| + | | \(\tau\) || \(\frac{m}{kn}\) | ||
| + | |} | ||
=Resolução de equações diferenciais lineares do segundo grau= | =Resolução de equações diferenciais lineares do segundo grau= | ||
Este tipo de equações aparece frequentemente em sistemas oscilatórios, como o oscilador harmónico (livre ou com atrito), que descreve o comportamento de sistemas físicos como o [https://pt.wikipedia.org/wiki/P%C3%AAndulo pêndulo] (no limite de pequenas oscilações) ou o [https://pt.wikipedia.org/wiki/Sistema_massa-mola sistema massa-mola]. Na ausência de atrito e de outras forças não conservativas, a equação envolve a segunda derivada e um termo linear do tipo | Este tipo de equações aparece frequentemente em sistemas oscilatórios, como o oscilador harmónico (livre ou com atrito), que descreve o comportamento de sistemas físicos como o [https://pt.wikipedia.org/wiki/P%C3%AAndulo pêndulo] (no limite de pequenas oscilações) ou o [https://pt.wikipedia.org/wiki/Sistema_massa-mola sistema massa-mola]. Na ausência de atrito e de outras forças não conservativas, a equação envolve a segunda derivada e um termo linear do tipo | ||
| − | <math> | + | <center><math> |
a \frac{d^2f}{dt^2} + bf = 0 | a \frac{d^2f}{dt^2} + bf = 0 | ||
| − | </math> | + | </math></center> |
em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a\) e \(b\) são constantes positivas. Reescrevendo: | em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a\) e \(b\) são constantes positivas. Reescrevendo: | ||
| − | <math> | + | <center><math> |
\frac{d^2f}{dt^2} = -\frac{b}{a}f | \frac{d^2f}{dt^2} = -\frac{b}{a}f | ||
| − | </math> | + | </math></center> |
| − | Podemos | + | Podemos exprimir a questão desta forma: ''qual a função (ou funções) cuja segunda derivada é igual à primeira, multiplicada por uma constante negativa''? É fácil verificar que há duas soluções possíveis: as funções seno e cosseno, ou seja, genericamente \(f(t)\) pode ter a forma geral |
| − | <math> | + | <center><math> |
f(t) = A \sin\left(\sqrt{\frac{b}{a}}t\right) + B \cos\left(\sqrt{\frac{b}{a}}t\right) | f(t) = A \sin\left(\sqrt{\frac{b}{a}}t\right) + B \cos\left(\sqrt{\frac{b}{a}}t\right) | ||
| − | </math> | + | </math></center> |
| + | |||
| + | onde \(A\) e \(B\) são duas constantes que é necessário introduzir; por enquanto são desconhecidas, mas podemos determiná-las se soubermos as condições iniciais do sistema – a posição inicial, a velocidade inicial, etc. | ||
| + | |||
| + | Vamos verificar que esta expressão é, de facto, a solução da equação diferencial acima. Para simplificar a escrita, definimos \(\omega_0 = \sqrt{\frac{b}{a}}\). Temos assim: | ||
| + | |||
| + | <center><math> | ||
| + | f(t) = A \sin(\omega_0 t) + B \cos(\omega_0 t) | ||
| + | </math></center> | ||
| + | |||
| + | <center><math> | ||
| + | \frac{df}{dt} = A \omega_0 \cos(\omega_0 t) - B \omega_0 \sin(\omega_0 t) | ||
| + | </math></center> | ||
| − | + | <center><math> | |
| + | \frac{d^2f}{dt^2} = -A \omega_0^2 \sin(\omega_0 t) - B \omega_0^2 \cos(\omega_0 t) = -\omega_0^2 f(t) = -\frac{b}{a}f | ||
| + | </math></center> | ||
| − | + | Vemos assim que a expressão encontrada é a solução da equação diferencial. É no entanto possível escrever esta expressão numa forma mais prática usando a seguinte igualdade trigonométrica | |
| − | |||
| − | |||
| − | + | <center><math> | |
| + | \sin(u+v)=\sin u\cos v+\cos u\sin v | ||
| + | </math></center> | ||
| − | <math> | + | Fazendo isto, a solução geral da equação pode ser escrita numa forma muito simples, e em vez de 𝐴 e 𝐵 ficamos com outras duas constantes mais intuitivas<ref>Pode verificar que é possível escrever a expressão deste modo, por exemplo calculando os valores de \(A_0\) e \(\phi_0\) a partir dos valores de \(A\) e \(B\). Sugestão: considere as expressões para \(f(0)\) e \(f'(0)\) num caso e noutro, e iguale-as respectivamente.</ref>: |
| + | |||
| + | <center><math> | ||
f(t) = A_0 \sin(\omega_0 t + \phi_0) | f(t) = A_0 \sin(\omega_0 t + \phi_0) | ||
| − | </math> | + | </math></center> |
| − | \ | + | Esta expressão permite verificar que a solução geral do oscilador harmónico livre tem as seguintes características: |
| + | * Varia no tempo de forma sinusoidal | ||
| + | * Tem uma frequência angular \(\omega\) e consequentemente um período \(T=2\pi/\omega\) | ||
| + | * A constante \(A_0\) é a amplitude máxima do movimento | ||
| + | * A constante \(\phi_0\) é a fase inicial do movimento | ||
| − | + | A tabela seguinte lista o valor de alguns dos principais parâmetros para o caso do pêndulo e do sistema massa-mola. | |
| − | |||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
| Linha 115: | Linha 169: | ||
| '''\(\omega_0\)''' || \(\sqrt{g/\ell}\) || \(\sqrt{k/m}\) | | '''\(\omega_0\)''' || \(\sqrt{g/\ell}\) || \(\sqrt{k/m}\) | ||
|} | |} | ||
| + | |||
| + | =Notas= | ||
Edição atual desde as 17h42min de 23 de janeiro de 2025
Derivadas parciais
Quando uma função depende de mais do que uma variável, é possível calcular a sua derivada segundo cada uma dessas variáveis. Por exemplo, uma função \(f \equiv f(x, y)\) que depende das variáveis \(x\) e \(y\) tem duas derivadas parciais:
- Derivada parcial segundo \(x:\,\frac{\partial f}{\partial x}\)
- Derivada parcial segundo \(y:\,\frac{\partial f}{\partial y}\)
Para calcular cada uma das derivadas parciais, tratam-se as outras variáveis como se fossem uma constante. Note que as derivadas parciais são assinaladas com o símbolo \(\partial\) em vez de \(d\).
Exemplos:
\begin{array}{rl} f(x, y)=x^3y^2 &\implies \frac{\partial f}{\partial x} = 3x^2y^2, \quad \frac{\partial f}{\partial y} = 2x^3y \\ f(x, y)=e^{-y}\sin(x) &\implies \frac{\partial f}{\partial x} = e^{-y}\cos(x), \quad \frac{\partial f}{\partial y} = -e^{-y}\sin(x) \end{array}
Resolução de equações diferenciais lineares do primeiro grau
Este tipo de equações aparece, por exemplo, em situações em que uma força (tipicamente o atrito) é proporcional à velocidade, tais como a queda de uma gotícula de óleo na Experiência de Millikan. A equação envolve a primeira derivada, um termo linear e um termo constante, e podemos escrever a seguinte expressão genérica:
em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a, b\) e \(c\) são constantes. Para resolver esta equação, vamos recorrer a uma função auxiliar \(g(t)\) definida como:
Se derivarmos esta igualdade verificamos que as derivadas de ambas as funções são iguais:
Inserindo estas duas igualdades na primeira equação, podemos escrevê-la na forma
A última igualdade apresenta-nos então a questão: qual a função cuja derivada é igual à própria função, multiplicada por uma constante? Não é difícil concluir que é a função exponencial, mais concretamente:
é a solução daquela equação, em que \(A\) é uma constante que é necessário introduzir, e que depende das condições iniciais do sistema. Agora que determinámos a solução para \(g(t)\), podemos calcular a função \(f(t)\) original:
Para determinar o valor de \(A\), temos que ter alguma informação sobre o sistema. Por exemplo, sabendo que o valor inicial da função \(f(t)\) é \(f(0) = f_0\), podemos escrever:
Inserindo esta expressão no valor de \(A\) e simplificando, temos finalmente a solução geral da equação original:
Quando \(t\rightarrow\infty\) a função atinge um valor limite \(f_{lim}=b/c\), independentemente do valor da velocidade inicial. Podemos ainda definir um “tempo médio” \(\tau=a/c\) para a função exponencial.
A tabela em baixo mostra a aplicação da resolução acima à Experiência de Millikan. A figura mostra a evolução de uma função \(v(t)\), solução de uma equação deste tipo, e resume a interligação entre todos os parâmetros apresentados. Note que os eixos são normalizados, isto é, os seus valores são divididos por constantes características do problema (neste caso, o tempo médio \(\tau\) e a velocidade limite \(v_{lim}\).
| Exp. Millikan | |
|---|---|
| Eq. diferencial | \(m \frac{dv}{dt} = mg - knv\) |
| Função \(f(t)\) | Velocidade \(v(t)\) |
| \(df/dt\) | Aceleração \(a(t) = dv/dt\) |
| \(a\) | \(m\) |
| \(b\) | \(mg\) |
| \(c\) | \(kn\) |
| \(A\) | \(f_0 = \text{Vel. inicial} = 0 \, \text{m/s}\) |
| Expressão | \(\frac{mg}{kn} \left[ 1 - \exp\left(-\frac{kn}{m}t\right) \right]\) |
| \(f_{\text{lim}}\) | \(v_{\text{lim}} = \frac{mg}{kn}\) |
| \(\tau\) | \(\frac{m}{kn}\) |
Resolução de equações diferenciais lineares do segundo grau
Este tipo de equações aparece frequentemente em sistemas oscilatórios, como o oscilador harmónico (livre ou com atrito), que descreve o comportamento de sistemas físicos como o pêndulo (no limite de pequenas oscilações) ou o sistema massa-mola. Na ausência de atrito e de outras forças não conservativas, a equação envolve a segunda derivada e um termo linear do tipo
em que \(f \equiv f(t)\) é uma função que só depende de uma variável \(t\) (por exemplo, o tempo) e \(a\) e \(b\) são constantes positivas. Reescrevendo:
Podemos exprimir a questão desta forma: qual a função (ou funções) cuja segunda derivada é igual à primeira, multiplicada por uma constante negativa? É fácil verificar que há duas soluções possíveis: as funções seno e cosseno, ou seja, genericamente \(f(t)\) pode ter a forma geral
onde \(A\) e \(B\) são duas constantes que é necessário introduzir; por enquanto são desconhecidas, mas podemos determiná-las se soubermos as condições iniciais do sistema – a posição inicial, a velocidade inicial, etc.
Vamos verificar que esta expressão é, de facto, a solução da equação diferencial acima. Para simplificar a escrita, definimos \(\omega_0 = \sqrt{\frac{b}{a}}\). Temos assim:
Vemos assim que a expressão encontrada é a solução da equação diferencial. É no entanto possível escrever esta expressão numa forma mais prática usando a seguinte igualdade trigonométrica
Fazendo isto, a solução geral da equação pode ser escrita numa forma muito simples, e em vez de 𝐴 e 𝐵 ficamos com outras duas constantes mais intuitivas[1]:
Esta expressão permite verificar que a solução geral do oscilador harmónico livre tem as seguintes características:
- Varia no tempo de forma sinusoidal
- Tem uma frequência angular \(\omega\) e consequentemente um período \(T=2\pi/\omega\)
- A constante \(A_0\) é a amplitude máxima do movimento
- A constante \(\phi_0\) é a fase inicial do movimento
A tabela seguinte lista o valor de alguns dos principais parâmetros para o caso do pêndulo e do sistema massa-mola.
| Pêndulo | Massa-mola | |
|---|---|---|
| Equação diferencial | \(\ddot{\theta} = -\frac{g}{\ell}\theta\) | \(\ddot{x} = -\frac{k}{m}x\) |
| Função \(f(t)\) | Ângulo \(\theta(t)\) | Posição \(x(t)\) |
| \(\ddot{f}\) | Acel. angular \(\alpha(t) = \ddot{\theta}\) | Aceleração \(a(t) = \ddot{x}\) |
| \(a\) | \(\ell\) | \(m\) |
| \(b\) | \(g\) | \(k\) |
| \(A_0\) | Amplitude máxima \(\theta_0\) | Amplitude máxima \(A_0\) |
| \(\phi_0\) | (fase inicial) | (fase inicial) |
| \(\omega_0\) | \(\sqrt{g/\ell}\) | \(\sqrt{k/m}\) |
Notas
- ↑ Pode verificar que é possível escrever a expressão deste modo, por exemplo calculando os valores de \(A_0\) e \(\phi_0\) a partir dos valores de \(A\) e \(B\). Sugestão: considere as expressões para \(f(0)\) e \(f'(0)\) num caso e noutro, e iguale-as respectivamente.