Diferenças entre edições de "Carga pontual dentro de uma esfera dielétrica"
Saltar para a navegação
Saltar para a pesquisa
(Criou a página com "Uma carga \(q\) está colocada no centro de uma esfera oca de raios interno \(R_1\) e externo \(R_2\). A esfera é constituída por um material dielétrico perfeito LHI, de...") |
|||
| Linha 1: | Linha 1: | ||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> | ||
| + | '''Metadata''' | ||
| + | <div class="mw-collapsible-content"> | ||
| + | *CONTEXTO : Primeiro ciclo universitário | ||
| + | *AREA: Física | ||
| + | *DISCIPLINA: Eletromagnetismo e Óptica | ||
| + | *ANO: 2 | ||
| + | *LINGUA: pt | ||
| + | *AUTOR: Jorge Loureiro | ||
| + | *MATERIA PRINCIPAL: Eletrostática na matéria | ||
| + | *DESCRICAO: Determinação do campo elétrico criado por uma carga pontual num dielétrico. | ||
| + | *DIFICULDADE: *** | ||
| + | *TEMPO MEDIO DE RESOLUCAO: 5 min | ||
| + | *TEMPO MAXIMO DE RESOLUCAO: 10 min | ||
| + | *PALAVRAS CHAVE: campo elétrico, cargas pontuais, dielétrico, Lei de Gauss | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | [[Ficheiro:Pr1_2E2_2015.png|thumb|right|middle|upright=0.75]] | ||
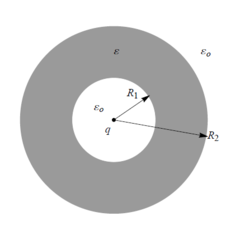
Uma carga \(q\) está colocada no centro de uma esfera oca de raios interno \(R_1\) e externo \(R_2\). | Uma carga \(q\) está colocada no centro de uma esfera oca de raios interno \(R_1\) e externo \(R_2\). | ||
A esfera é constituída por um material dielétrico perfeito LHI, de permitividade elétrica \( \epsilon > \epsilon_0 \), e está inicialmente descarregada. | A esfera é constituída por um material dielétrico perfeito LHI, de permitividade elétrica \( \epsilon > \epsilon_0 \), e está inicialmente descarregada. | ||
#Determine o campo elétrico \( \boldsymbol{E_e} \) em todas as regiões do espaço, e o potencial elétrico na superfície interna da esfera dielétrica. | #Determine o campo elétrico \( \boldsymbol{E_e} \) em todas as regiões do espaço, e o potencial elétrico na superfície interna da esfera dielétrica. | ||
#Assuma agora que a esfera dielétrica se encontra uniformemente eletrizada em volume, com uma carga elétrica total \(-q\). Determine o novo valor do campo \( \boldsymbol{E_e} \) em todos os pontos do espaço e as densidades de carga de polarização. Verifique que a carga total de polarização é nula. | #Assuma agora que a esfera dielétrica se encontra uniformemente eletrizada em volume, com uma carga elétrica total \(-q\). Determine o novo valor do campo \( \boldsymbol{E_e} \) em todos os pontos do espaço e as densidades de carga de polarização. Verifique que a carga total de polarização é nula. | ||
Edição atual desde as 17h37min de 17 de setembro de 2015
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Eletromagnetismo e Óptica
- ANO: 2
- LINGUA: pt
- AUTOR: Jorge Loureiro
- MATERIA PRINCIPAL: Eletrostática na matéria
- DESCRICAO: Determinação do campo elétrico criado por uma carga pontual num dielétrico.
- DIFICULDADE: ***
- TEMPO MEDIO DE RESOLUCAO: 5 min
- TEMPO MAXIMO DE RESOLUCAO: 10 min
- PALAVRAS CHAVE: campo elétrico, cargas pontuais, dielétrico, Lei de Gauss
Uma carga \(q\) está colocada no centro de uma esfera oca de raios interno \(R_1\) e externo \(R_2\). A esfera é constituída por um material dielétrico perfeito LHI, de permitividade elétrica \( \epsilon > \epsilon_0 \), e está inicialmente descarregada.
- Determine o campo elétrico \( \boldsymbol{E_e} \) em todas as regiões do espaço, e o potencial elétrico na superfície interna da esfera dielétrica.
- Assuma agora que a esfera dielétrica se encontra uniformemente eletrizada em volume, com uma carga elétrica total \(-q\). Determine o novo valor do campo \( \boldsymbol{E_e} \) em todos os pontos do espaço e as densidades de carga de polarização. Verifique que a carga total de polarização é nula.