Diferenças entre edições de "Integral de curva parametrizada"
Saltar para a navegação
Saltar para a pesquisa
(Criou a página com "<div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> '''Metadata''' <div class="mw-collapsible-content"> *CONTEXTO : Primeiro ciclo universitário *AREA:...") |
|||
| (Há 2 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 7: | Linha 7: | ||
*ANO: 1 | *ANO: 1 | ||
*LINGUA: pt | *LINGUA: pt | ||
| − | *AUTOR: | + | *AUTOR: Ana Moura Santos e Miguel Dziergwa |
*MATERIA PRINCIPAL: Integrais de linha: integrais de campos escalares e campos vetoriais | *MATERIA PRINCIPAL: Integrais de linha: integrais de campos escalares e campos vetoriais | ||
*DESCRICAO: Integral de curva parametrizada | *DESCRICAO: Integral de curva parametrizada | ||
| − | *DIFICULDADE: | + | *DIFICULDADE: ** |
*TEMPO MEDIO DE RESOLUCAO: 15 mn | *TEMPO MEDIO DE RESOLUCAO: 15 mn | ||
*TEMPO MAXIMO DE RESOLUCAO: 30 mn | *TEMPO MAXIMO DE RESOLUCAO: 30 mn | ||
| Linha 32: | Linha 32: | ||
| − | Para obter o zip que contém as instâncias deste exercício clique aqui | + | Para obter o zip que contém as instâncias deste exercício clique aqui[https://drive.tecnico.ulisboa.pt/api/drive/file/1695923671483517/download] |
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | ||
Edição atual desde as 14h30min de 4 de abril de 2018
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo diferencial e integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Integrais de linha: integrais de campos escalares e campos vetoriais
- DESCRICAO: Integral de curva parametrizada
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE:
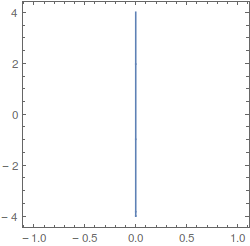
Sejam a função escalar \(f\)\(\left(\begin{array}{c}x\\y\\\end{array}\right)\)=\(-5x-4y\) e a curva parametrizada por \( \gamma = \)\(\left(\begin{array}{c}0\\-4t\\\end{array}\right)\). A representação geométrica da imagem de \( \gamma \) com \(t\text{$\in$[}-1,1]\) encontra-se na figura abaixo.
O integral de \(f\) com respeito ao arco da curva parametrizada por \( \gamma \) em \([-1,1]\) é igual a:
A) \(0\)
B) \(8\)
C) \(16\)
D) \(-16\)
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt