Diferenças entre edições de "Pêndulo Cónico"
Saltar para a navegação
Saltar para a pesquisa
(Criou a página com "<div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> '''Metadata''' <div class="mw-collapsible-content"> *CONTEXTO : Primeiro ciclo universitário *AREA:...") |
|||
| (Há 12 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 17: | Linha 17: | ||
</div> | </div> | ||
| + | [[File:Pendulo_conico.png|thumb|Sistema em estudo.]] | ||
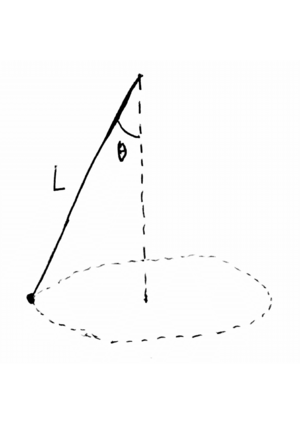
| − | Considere o pêndulo cónico representado na figura | + | Considere o pêndulo cónico representado na figura. O movimento do pêndulo verifica-se no plano xy. O comprimento do fio é L e o fio faz um ângulo θ com a vertical. |
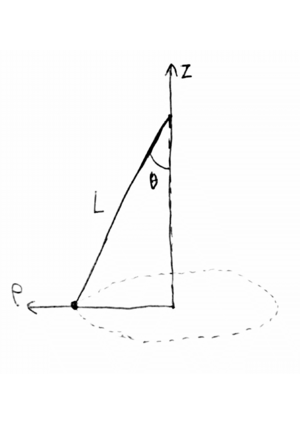
* Escolha um sistema de coordenadas para estudar o movimento do pêndulo. | * Escolha um sistema de coordenadas para estudar o movimento do pêndulo. | ||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width: | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px"> |
'''Respostas''' | '''Respostas''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | + | [[File:Pendulo_conico_frame.png|frameless|]] | |
</div> | </div> | ||
| Linha 33: | Linha 34: | ||
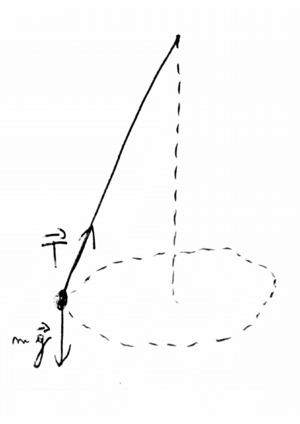
* Represente as forças que actuam no pêndulo. | * Represente as forças que actuam no pêndulo. | ||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width: | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px"> |
'''Respostas''' | '''Respostas''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | + | [[File:Pendulo_conico_forcas.png|frameless|]] | |
| + | |||
| + | As forças que actuam no pêndulo são a tensão (T) do fio e o peso (mg) da massa. | ||
</div> | </div> | ||
| Linha 44: | Linha 47: | ||
* Calcule a expressão para a aceleração centrípeta do pêndulo. | * Calcule a expressão para a aceleração centrípeta do pêndulo. | ||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width: | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px"> |
'''Respostas''' | '''Respostas''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Linha 53: | Linha 56: | ||
</div> | </div> | ||
| − | * Mostre que o módulo da velocidade do pêndulo é dado por: \(v = \sqrt{g L \sin{\theta} \tan{\theta}}\) | + | * Mostre que o módulo da velocidade do pêndulo é dado por: |
| + | \(v = \sqrt{g L \sin{\theta} \tan{\theta}}\) | ||
* Calcule a velocidade angular e o período do pêndulo. | * Calcule a velocidade angular e o período do pêndulo. | ||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width: | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px"> |
'''Respostas''' | '''Respostas''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Linha 63: | Linha 67: | ||
* \(\omega = \sqrt{\frac{g}{L \cos{\theta}}}\) | * \(\omega = \sqrt{\frac{g}{L \cos{\theta}}}\) | ||
| − | * \( T = 2 \pi \sqrt{\frac{L \cos{\theta}}{g}} | + | * \( T = 2 \pi \sqrt{\frac{L \cos{\theta}}{g}}\) |
</div> | </div> | ||
</div> | </div> | ||
Edição atual desde as 11h25min de 24 de fevereiro de 2016
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Mecânica e ondas
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Mourão
- MATERIA PRINCIPAL: Dinâmica do Ponto Material
- DESCRICAO: Pêndulo Cónico
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 600 [s]
- TEMPO MAXIMO DE RESOLUCAO: 1200 [s]
- PALAVRAS CHAVE: gravidade, forças, Tensão, pêndulo, cónico
Considere o pêndulo cónico representado na figura. O movimento do pêndulo verifica-se no plano xy. O comprimento do fio é L e o fio faz um ângulo θ com a vertical.
- Escolha um sistema de coordenadas para estudar o movimento do pêndulo.
- Represente as forças que actuam no pêndulo.
- Calcule a expressão para a aceleração centrípeta do pêndulo.
Respostas
- \(a_c = g \tan{\theta}\)
- Mostre que o módulo da velocidade do pêndulo é dado por:
\(v = \sqrt{g L \sin{\theta} \tan{\theta}}\)
- Calcule a velocidade angular e o período do pêndulo.
Respostas
- \(\omega = \sqrt{\frac{g}{L \cos{\theta}}}\)
- \( T = 2 \pi \sqrt{\frac{L \cos{\theta}}{g}}\)