Diferenças entre edições de "Par aleatório discreto - covariância"

Fonte: My Solutions
Saltar para a navegação Saltar para a pesquisa
(Criou a página com "<div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> '''Metadata''' <div class="mw-collapsible-content"> *CONTEXTO : Primeiro ciclo universitário *AREA:...")
 
Linha 17: Linha 17:
 
</div>
 
</div>
  
−
Considere a seguinte função de probabilidade conjunta do par aleatório (X,Y): P(X=4,Y=1)=0 , P(X=4,Y=3)=\(0.4\) , \(P(X=\)\(4\)\(,Y=\)4)=\(0\) , P(X=6,Y=1)=0.3 , P(X=6,Y=3)=0.2 , P(X=6,Y=4)=0.1. E zero nos restantes casos.
+
Considere a seguinte função de probabilidade conjunta do par aleatório \( (X, Y) \):  
−
Calcule a covariância entre X e Y.
+
[[File:CovarTable.gif]]
 +
Calcule a covariância entre X e Y.
  
 
A resposta correcta é: A)−0.4 , B)0.25 , C)0.96 , D)5.2
 
A resposta correcta é: A)−0.4 , B)0.25 , C)0.96 , D)5.2

Revisão das 10h15min de 11 de abril de 2017

Metadata

  • CONTEXTO : Primeiro ciclo universitário
  • AREA: Matemática
  • DISCIPLINA: Probabilidades e Estatística
  • ANO: 2
  • LINGUA: pt
  • AUTOR: Equipa de Probabilidades e Estatística
  • MATERIA PRINCIPAL: Distribuições conjuntas de probabilidade e complementos
  • DESCRICAO: Par aleatório discreto - covariância
  • DIFICULDADE: *
  • TEMPO MEDIO DE RESOLUCAO: 10 min
  • TEMPO MAXIMO DE RESOLUCAO: 15 min
  • PALAVRAS CHAVE: par aleatório discreto, função de probabilidade conjunta, covariância

Considere a seguinte função de probabilidade conjunta do par aleatório (X,Y): 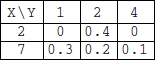CovarTable.gif Calcule a covariância entre X e Y.

A resposta correcta é: A)−0.4 , B)0.25 , C)0.96 , D)5.2


Para obter o zip que contém as instâncias deste exercício clique aqui[1]

Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt

Obtida de "http://www.mysolutions.tecnico.ulisboa.pt//wiki/index.php?title=Par_aleatório_discreto_-_covariância&oldid=3012"