Diferenças entre edições de "Vetor combinação linear em \(R^2\)"
| Linha 16: | Linha 16: | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
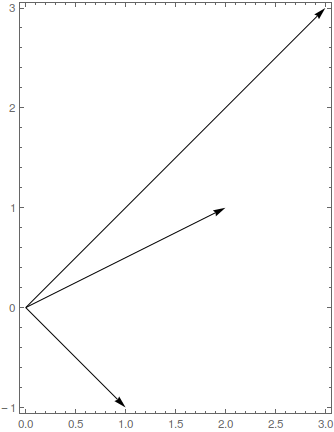
| − | + | Considere os vectores \(\pmb{v_1}\)=\(\left(\begin{array}{c}-1\\-2\\\end{array}\right)\),\(\pmb{v_2}\)=\(\left(\begin{array}{c}-3\\4\\\end{array}\right)\) e \(\pmb{v_3}\)=\(\left(\begin{array}{c}5\\0\\\end{array}\right)\) da figura seguinte: | |
| + | |||
[[File:CombLinear.gif]] | [[File:CombLinear.gif]] | ||
| − | + | Determine primeiro os valores dos coeficientes \(a_1\) e \(a_2\) tais que o vector \(\pmb{v_1}\) se escreve como uma combinação linear dos vectores \(\pmb{v_1}\) e \(\pmb{v_2}\), isto é, \(\pmb{v_3}\) = \(a_1 \times \)\(\pmb{v_1}\) +\( a_2 \times\) \(\pmb{v_2}\). A soma \(a_1 +a_2\) é igual a : | |
| − | |||
| − | Determine primeiro os valores dos coeficientes \(a_1\) e \(a_2\) tais que o vector \(\ | ||
A)\(1\), | A)\(1\), | ||
Revisão das 14h47min de 23 de agosto de 2016
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Álgebra Linear
- ANO: 1
- LINGUA: pt
- AUTOR: Equipa Álgebra Linear
- MATERIA PRINCIPAL:
- DESCRICAO:
- DIFICULDADE:
- TEMPO MEDIO DE RESOLUCAO:
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE:
Considere os vectores \(\pmb{v_1}\)=\(\left(\begin{array}{c}-1\\-2\\\end{array}\right)\),\(\pmb{v_2}\)=\(\left(\begin{array}{c}-3\\4\\\end{array}\right)\) e \(\pmb{v_3}\)=\(\left(\begin{array}{c}5\\0\\\end{array}\right)\) da figura seguinte:
Determine primeiro os valores dos coeficientes \(a_1\) e \(a_2\) tais que o vector \(\pmb{v_1}\) se escreve como uma combinação linear dos vectores \(\pmb{v_1}\) e \(\pmb{v_2}\), isto é, \(\pmb{v_3}\) = \(a_1 \times \)\(\pmb{v_1}\) +\( a_2 \times\) \(\pmb{v_2}\). A soma \(a_1 +a_2\) é igual a :
A)\(1\), B)\(8\), C)\(-9\), D)\(7\)
Para obter o zip que contém as instâncias deste exercício clique aqui(comblinear.nb)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt