Diferenças entre edições de "Óptica geométrica e lentes"
(Criou a página com "=Óptica geométrica e lentes= Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um ''objecto'' numa dada posição, c...") |
m |
||
| Linha 1: | Linha 1: | ||
| − | |||
Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um ''objecto'' numa dada posição, como desenhar um sistema óptico que permita transferir uma ''imagem'' desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas. | Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um ''objecto'' numa dada posição, como desenhar um sistema óptico que permita transferir uma ''imagem'' desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas. | ||
| Linha 8: | Linha 7: | ||
Neste documento apresentamos uma introdução à elaboração de construções geométricas usando lentes delgadas. | Neste documento apresentamos uma introdução à elaboração de construções geométricas usando lentes delgadas. | ||
| − | + | =Aproximações= | |
[[file:OG-definicoes.png|thumb|upright=0.5 | Fig. 4 - Definições utilizadas.]] | [[file:OG-definicoes.png|thumb|upright=0.5 | Fig. 4 - Definições utilizadas.]] | ||
Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar: | Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar: | ||
| Linha 20: | Linha 19: | ||
A Fig. 4 ilustra a geometria relevante para estas definições, sendo \(f\) a distância focal, \(d\ll f\) a espessura da lente delgada e \(\alpha\) o ângulo entre o raio e o eixo óptico. | A Fig. 4 ilustra a geometria relevante para estas definições, sendo \(f\) a distância focal, \(d\ll f\) a espessura da lente delgada e \(\alpha\) o ângulo entre o raio e o eixo óptico. | ||
| − | + | =Convenções= | |
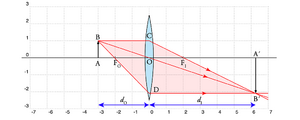
[[file:OG-convencoes.png|thumb|upright=1.0 |Fig. 5 - Convenções utilizadas para formação de imagens por lentes.]] | [[file:OG-convencoes.png|thumb|upright=1.0 |Fig. 5 - Convenções utilizadas para formação de imagens por lentes.]] | ||
A Fig. 5 ilustra os principais parâmetros do traçado de raios através de uma lente simples. | A Fig. 5 ilustra os principais parâmetros do traçado de raios através de uma lente simples. | ||
| Linha 42: | Linha 41: | ||
De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas. | De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas. | ||
| − | + | =Objecto e imagem: focos conjugados e ampliação transversal= | |
Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições ''focos conjugados''. | Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições ''focos conjugados''. | ||
Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem: | Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem: | ||
| Linha 83: | Linha 82: | ||
Como exemplo, temos no caso da Fig. 5: \(d_O>f \to A> 0\,; d_I > 0\). A imagem resultante é ‘’real’’ e ‘’invertida’’. | Como exemplo, temos no caso da Fig. 5: \(d_O>f \to A> 0\,; d_I > 0\). A imagem resultante é ‘’real’’ e ‘’invertida’’. | ||
| − | + | =Lente convergente (\(f>0\))= | |
| − | + | ==Imagem real== | |
Este caso verifica-se para \(d_O>f\), a imagem é real é pode ser projectada. A imagem é menor (\(A<1\)) que o objecto se \(d_O>2f\) ou maior (\(A>1\)) se \(2f>d_O>0\). Um exemplo do primeiro caso é uma máquina fotográfica: a imagem é posicionada no sensor da câmara, e é (tipicamente) menor que o objecto fotografado. Verifica-se \(0 < A \le 1\) pois | Este caso verifica-se para \(d_O>f\), a imagem é real é pode ser projectada. A imagem é menor (\(A<1\)) que o objecto se \(d_O>2f\) ou maior (\(A>1\)) se \(2f>d_O>0\). Um exemplo do primeiro caso é uma máquina fotográfica: a imagem é posicionada no sensor da câmara, e é (tipicamente) menor que o objecto fotografado. Verifica-se \(0 < A \le 1\) pois | ||
| Linha 98: | Linha 97: | ||
</math> | </math> | ||
| − | + | ==Imagem virtual== | |
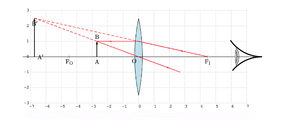
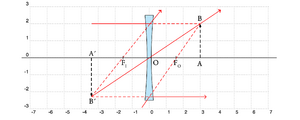
[[file:OG-convvirt0.png|thumb|upright=1.0 |Fig. 6 - Formação de imagem virtual com uma lente convergente.]] | [[file:OG-convvirt0.png|thumb|upright=1.0 |Fig. 6 - Formação de imagem virtual com uma lente convergente.]] | ||
Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações | Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações | ||
| Linha 109: | Linha 108: | ||
Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (''i'') virtual e (''ii'') direita, para um observador colocado à direita da lente. | Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (''i'') virtual e (''ii'') direita, para um observador colocado à direita da lente. | ||
| − | + | =Lente divergente (\(f<0\))= | |
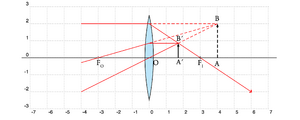
[[file:OG-divvirt.png|thumb|upright=1.0 |Fig. 7 - Formação de imagem virtual com uma lente divergente.]] | [[file:OG-divvirt.png|thumb|upright=1.0 |Fig. 7 - Formação de imagem virtual com uma lente divergente.]] | ||
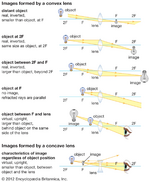
[[file:OG-Ray-diagrams-types-lenses-length.png|thumb|upright=0.5 |Fig. 8 - Tabela resumo para lentes convergentes e divergentes.]] | [[file:OG-Ray-diagrams-types-lenses-length.png|thumb|upright=0.5 |Fig. 8 - Tabela resumo para lentes convergentes e divergentes.]] | ||
| Linha 130: | Linha 129: | ||
A Fig. 8 apresenta uma tabela resumo de todas as situações analisadas acima. | A Fig. 8 apresenta uma tabela resumo de todas as situações analisadas acima. | ||
| − | + | =Objectos virtuais= | |
Em determinadas situações, podemos lidar com ''objectos virtuais'' (\(d_O<0\)), isto é, os raios ópticos têm origem não num objecto sólido, mas num plano do espaço, e estamos interessados em estudar a sua propagação a partir desse plano e a formação da imagem correspondente. Um exemplo típico consiste em estudar a formação da imagem de uma imagem primária. Nestes casos, o objecto virtual é identificado a tracejado no diagrama de raios, como ilustrado nos exemplos em baixo. | Em determinadas situações, podemos lidar com ''objectos virtuais'' (\(d_O<0\)), isto é, os raios ópticos têm origem não num objecto sólido, mas num plano do espaço, e estamos interessados em estudar a sua propagação a partir desse plano e a formação da imagem correspondente. Um exemplo típico consiste em estudar a formação da imagem de uma imagem primária. Nestes casos, o objecto virtual é identificado a tracejado no diagrama de raios, como ilustrado nos exemplos em baixo. | ||
| − | + | ==Lente convergente \(f>0\)== | |
[[file:OG-convvirt.png|thumb|upright=1.0 |Fig. 9 - Lente convergente com objecto virtual e imagem real.]] | [[file:OG-convvirt.png|thumb|upright=1.0 |Fig. 9 - Lente convergente com objecto virtual e imagem real.]] | ||
A Fig. 9 representa um objecto virtual (\(d_O<0\), à direita da lente) e a correspondente imagem. A imagem resultante é real (\(d_I>0\), também à direita) e direita (\(A<0\)), verificando-se | A Fig. 9 representa um objecto virtual (\(d_O<0\), à direita da lente) e a correspondente imagem. A imagem resultante é real (\(d_I>0\), também à direita) e direita (\(A<0\)), verificando-se | ||
| Linha 143: | Linha 142: | ||
\end{array} | \end{array} | ||
| − | + | ==Lente divergente \(f<0\) - Imagem virtual== | |
[[file:OG-divvirtvirt.png|thumb|upright=1.0 |Fig. 10 - Lente divergente com objecto virtual e imagem virtual.]] | [[file:OG-divvirtvirt.png|thumb|upright=1.0 |Fig. 10 - Lente divergente com objecto virtual e imagem virtual.]] | ||
A Fig. 10 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à direita do foco \(F_O\): \(|d_O|>|f|\). Verifica-se assim: | A Fig. 10 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à direita do foco \(F_O\): \(|d_O|>|f|\). Verifica-se assim: | ||
| Linha 165: | Linha 164: | ||
</math> | </math> | ||
| − | + | ==Lente divergente \(f>0\) - Imagem real== | |
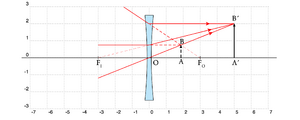
[[file:OG-divvirtreal.png|thumb|upright=1.0 |Fig. 11 - Lente divergente com objecto virtual e imagem real.]] | [[file:OG-divvirtreal.png|thumb|upright=1.0 |Fig. 11 - Lente divergente com objecto virtual e imagem real.]] | ||
A Fig. 11 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à esquerda do foco \(F_O\): \(|d_O|<|f|\). Verifica-se assim: | A Fig. 11 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à esquerda do foco \(F_O\): \(|d_O|<|f|\). Verifica-se assim: | ||
Revisão das 13h15min de 30 de janeiro de 2025
Uma das principais aplicações da óptica geométrica consiste no estudo da formação de imagens: dado um objecto numa dada posição, como desenhar um sistema óptico que permita transferir uma imagem desse objecto para uma posição diferente? É um problema que tem aplicações desde o olho humano até ao desenho de lentes e fibras ópticas.
Uma lente é um dos principais elementos usados em sistemas ópticos, e consiste tipicamente num sólido transparente com duas superfícies esféricas. Dependendo da curvatura destas superfícies, uma lente pode ser usada para aumentar ou diminuir o tamanho de um objecto, ou trazê-los objectos distantes para o ponto focal. As lentes são usadas por exemplo em óculos, câmaras, microscópios, telescópios e muitos outros sistemas de formação de imagem.
Um objecto iluminado uniformemente é considerado como uma fonte de raios, emitidos em todas as direcções. Podemos escolher um ponto no objecto e um conjunto adequado de raios, e traçar o seu percurso através do sistema até encontrar o correspondente ponto na imagem. Por convenção, desenha-se o sistema óptico em torno de um eixo, que coincide com o seu eixo geométrico, e os raios propagam-se da esquerda para a direita.
Neste documento apresentamos uma introdução à elaboração de construções geométricas usando lentes delgadas.
Aproximações
Utilizaremos as duas seguintes aproximações comuns, que facilitam grandemente os cálculos a efectuar:
| Lentes delgadas | Uma lente é considerada ‘’delgada’’ quando a sua espessura \(d\) é desprezável face à sua distância focal \(f\). |
| Aproximação paraxial | Admitimos que todos os raios envolvidos são paraxiais, isto é, (i) situam-se próximo do eixo óptico e (ii) o ângulo \(\alpha\) que fazem com esse eixo permite utilizar as aproximações \(\sin \alpha \approx \alpha\) e \(\tan \alpha \approx \alpha\,\), tipicamente válidas para \(\alpha \lesssim 5^{\circ}\). |
A Fig. 4 ilustra a geometria relevante para estas definições, sendo \(f\) a distância focal, \(d\ll f\) a espessura da lente delgada e \(\alpha\) o ângulo entre o raio e o eixo óptico.
Convenções
A Fig. 5 ilustra os principais parâmetros do traçado de raios através de uma lente simples.
- O objecto \(AB\) fica (por definição) do lado esquerdo da lente, a uma distância \(d_O>0\) desta; caso o objecto esteja do lado direito, temos \(d_O<0\) (que é o caso do objecto virtual abordado mais à frente)
- A imagem \(A'B'\) está do lado direito da lente, a uma distância \(d_I>0\) desta; caso a imagem esteja do lado esquerdo, temos \(d_I<0\)
- \(F_0\) é a distância focal do lado do objecto, \(F_I\) é a distância focal do lado da imagem. No caso de uma lente fina, ambas são iguais a \(f\), e marcam-se para auxiliar no traçado.
O raios ópticos que emergem de um dado objecto atravessam a lente e dão origem a uma imagem. A tabela em baixo descreve as propriedades dos dois tipos de imagens possíveis.
| Imagens reais | Os raios de luz passam de facto na posição da imagem, isto é, raios que saem do plano do objecto convergem no plano da imagem
Podem ser projectadas num alvo |
| Imagens virtuais | Os raios não passam na imagem, mas esta é visível através da lente
Não podem ser projectadas num alvo |
As imagens reais são, por exemplo, as criadas por um dispositivo de projecção. Um exemplo de imagem virtual é considerar a imagem de uma lâmpada brilhante: ao passar a mão pelo plano da imagem, se estar for real sente-se o calor, mas se for virtual parecerá apenas "flutuar" no espaço.
De seguida, vamos analisar a formação de imagens para lentes convergentes (\(f>0\)) e divergentes (\(f<0\)) em função da posição relativa do objecto e do foco da lente, e derivar relações úteis para lentes delgadas.
Objecto e imagem: focos conjugados e ampliação transversal
Considere de novo a Fig. 5. Cada ponto do objecto em \(d_O\) tem um único ponto correspondente na imagem em \(d_I\). Isto implica que, caso colocássemos o objecto em \(d_I\), a imagem seria formada em \(d_O\). Chama-se a estas posições focos conjugados. Pela semelhança de triângulos, temos as seguintes relações entre as dimensões do objecto e da imagem:
\begin{array}{lcl} \Delta ABF_O \sim \Delta ODF_O &\to & AB/A'B' = AF_O / F_O 0 &\to & AB/A'B' = \frac{d_O-f}{ f} \\ \Delta ABO\sim \Delta A'B'O &\to & AB/A'B' = AO / O A' &\to & AB/A'B' = d_O / d_I \\ \Delta COF_I \sim \Delta A'B'F_I &\to & AB/A'B' = OF_I / F_I A' &\to & AB/A'B' = \frac{f}{ d_I-f} \end{array}
Combinando a primeira e a última das expressões acima obtemos a equação dos focos conjugados:
| [math] \frac{1}{f} = \frac{1}{d_O} +\frac{1}{d_I} [/math] |
Uma forma alternativa e muitas vezes conveniente de exprimir esta relação consiste em utilizar as distâncias do objecto e da imagem aos respectivos focos. Designando estas distâncias por \(x_O=AF_O\) e \(x_I=A'F_I\), tem-se \(d_O=f+x_O\) e \(d_I=f+x_I\). Substituindo na expressão acima, obtém-se a chamada formulação de Newton para a equação dos focos conjugados:
| [math] x_Ox_I = f^2 [/math] |
Por outro lado, sendo \(AB\) e \(A'B'\)respectivamente as dimensões lineares transversais do objecto e da imagem, usamos a segunda das igualdades acima para definir a ‘’ampliação transversal’’ \(A\) como:
| [math] A = \frac{A'B'}{ AB} =\frac{d_I}{d_O} [/math] |
A imagem é ‘’direita’’ se \(A<0\) e ‘’invertida’’ se \(A>0\). Podemos usar estas duas equações para, dados \(f\)e \(d_O\), determinar as seguintes expressões para a posição da imagem \(d_I\)e a respectiva ampliação \(A\):
\begin{eqnarray} A&=&\frac{1}{\frac{d_O}{f}-1}\\ d_I&=&d_OA \end{eqnarray}
Como exemplo, temos no caso da Fig. 5: \(d_O>f \to A> 0\,; d_I > 0\). A imagem resultante é ‘’real’’ e ‘’invertida’’.
Lente convergente (\(f>0\))
Imagem real
Este caso verifica-se para \(d_O>f\), a imagem é real é pode ser projectada. A imagem é menor (\(A<1\)) que o objecto se \(d_O>2f\) ou maior (\(A>1\)) se \(2f>d_O>0\). Um exemplo do primeiro caso é uma máquina fotográfica: a imagem é posicionada no sensor da câmara, e é (tipicamente) menor que o objecto fotografado. Verifica-se \(0 < A \le 1\) pois
[math] \infty \gt d_O \ge 2 f \quad \to \quad f \lt d_I \le 2 f \quad \to \quad 0 \lt A\le 1 [/math]
Um exemplo do segundo caso é um projetor de cinema ou de imagem de computador: a imagem é posicionada num écran, e é maior que o objecto (película ou chip). Verifica-se \(1 \le A < \infty\) pois
[math] f \lt d_O \le 2 f \quad \to \quad \infty \gt d_I \ge 2f \quad \to \quad \infty \gt A\ge 1 [/math]
Imagem virtual
Este caso verifica-se quando \(d_O<f\), por exemplo quando utilizamos uma lupa para ver objectos com um tamanho aumentado, e está esquematizada na Fig. 6. Dependendo da posição \(d_O\), verificam-se as seguintes relações
\begin{array}{lcl} 0 < d_O \le \frac{f}{2} \qquad & 0 > d_I \ge -f \quad& -1 >A \ge -2\\ \frac{f}{2} \le d_O < f \qquad& -f\ge d_I >-\infty \quad& -2 > A > -\infty \end{array}
Repare-se que resulta \(d_I<0\) (a imagem está do mesmo lado que o objecto) e \(A<0\) pelo que a imagem é (i) virtual e (ii) direita, para um observador colocado à direita da lente.
Lente divergente (\(f<0\))
Considere-se a situação representada na Fig. 7, que mostra uma lente divergente (\(f<0\)) e um objecto \(AB\) (\(d_O>0\)). Note-se que, no caso da lente divergente, os pontos \(F_O\)e \(F_I\) trocam de posição. Nesta configuração a imagem resultante \(A'B'\) é sempre virtual e direita com \(d_I <0\) (imagem do mesmo lado do objeto), pois
[math] f\lt0; \quad d_O\gt 0 \quad \to \quad A\lt0; \quad d_I \lt0 [/math]
Podemos verificar que a equação dos focos conjugados se mantém válida neste caso, recorrendo à semelhança de triângulos:
\begin{array}{lcl} \Delta ABO \sim \Delta A'B'O & \to & AB/A'B' = \frac{d_0}{d_I} & \to & -\infty < A < 0 \\ \Delta ABF_0\sim \Delta ODF_O &\to & \frac{d_0 + |f|}{|f|} = AB/A'B' & \to & \frac{d_0 + |f|}{|f|} = \frac{d_0 }{d_I} \\ \Delta F_I OC \sim \Delta F_I A'B' &\to & \frac{|f|}{|f| - |d_I|} =AB/A'B' & \to & \frac{|f|}{|f| - |d_I|} = \frac{d_0 }{|d_I|} \end{array}
Nestas expressões, que descrevem distâncias, foi necessário utilizar os valores em módulo de \(f\) e de \(d_I\), que são ambos negativos. Fazendo agora as substituições \(|f|\to -f\) e \(|d_I|\to -d_I\) recupera-se a equação dos focos conjugados.
A Fig. 8 apresenta uma tabela resumo de todas as situações analisadas acima.
Objectos virtuais
Em determinadas situações, podemos lidar com objectos virtuais (\(d_O<0\)), isto é, os raios ópticos têm origem não num objecto sólido, mas num plano do espaço, e estamos interessados em estudar a sua propagação a partir desse plano e a formação da imagem correspondente. Um exemplo típico consiste em estudar a formação da imagem de uma imagem primária. Nestes casos, o objecto virtual é identificado a tracejado no diagrama de raios, como ilustrado nos exemplos em baixo.
Lente convergente \(f>0\)
A Fig. 9 representa um objecto virtual (\(d_O<0\), à direita da lente) e a correspondente imagem. A imagem resultante é real (\(d_I>0\), também à direita) e direita (\(A<0\)), verificando-se
\begin{array}{lcl} d_O < 0 ; \quad && f > 0 \quad \to \quad A<0\\ \frac{d_I}{-|d_O|} & =& \frac{f}{-|d_O| -f} \end{array}
Lente divergente \(f<0\) - Imagem virtual
A Fig. 10 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à direita do foco \(F_O\): \(|d_O|>|f|\). Verifica-se assim:
\begin{array}{lcl} d_O < 0 & & f < 0 \\ \frac{d_I}{|d_O|} & =& \frac{|f|}{|d_O| -|f|} \end{array}
A imagem resultante é também virtual \(d_I<0\), à esquerda da lente) e invertida (\(A>0\)), verificando-se as seguintes relações em função da distância:
[math] |d_O| = \left\{ \begin{array}{rl} |d_O| = |f|: & |d_I| \to \infty, \quad A \to \infty ,\\ |f| \lt |d_O| \lt 2|f|: & |d_I| \gt |d_O| , \quad A \gt1 ,\\ |d_O| = 2|f|: & |d_I| = |d_O|, \quad A =1 ,\\ |d_O| \gt 2|f|: & |d_I| \lt|d_O| , \quad 0 \lt A \lt1 . \end{array} \right. %f\lt0 \quad \to d_O\gt 0 ; \quad d_I \lt0 [/math]
Lente divergente \(f>0\) - Imagem real
A Fig. 11 representa um objecto virtual (\(d_O<0\), à direita da lente) para uma lente divergente (\(f<0\)) e a correspondente imagem. Na situação da figura, o objecto está à esquerda do foco \(F_O\): \(|d_O|<|f|\). Verifica-se assim:
\begin{array}{lcl} d_O < 0 & & f < 0 \nonumber\\ \frac{d_I}{|d_O|} & =& \frac{|f|}{|f|-|d_O|} \quad \to \quad A=\frac{d_I}{d_O} =\frac{f}{d_O-f}<0 \nonumber \end{array}
A imagem resultante é agora real (\(d_I>0\), à direita da lente) e direita (\(A<0\)), verificando-se as seguintes relações em função da distância:
[math] |d_O| = \left\{ \begin{array}{rl} |d_O| \to |f|: & |d_I| \to \infty, \quad A \to -\infty ,\\ |d_O| = |f|/2: & |d_I| = f, \quad A =-2 ,\\ |d_O| =0: & |d_I| =0 , \quad A=-1. \end{array} \right. %f\lt0 \quad \to d_O\gt 0 ; \quad d_I \lt0 [/math]