Diagonal de um paralelipípedo (coseno de um ângulo)

Metadata

• CONTEXTO : Primeiro ciclo universitário
• AREA: Matemática
• DISCIPLINA: Calculo Diferencial e Integral 2
• ANO: 1
• LINGUA: pt
• AUTOR: Ana Moura Santos e Miguel Dziergwa
• MATERIA PRINCIPAL: Estrutura algébrica e topológica de \(R^n\)
• DESCRICAO: Diagonal de um paralelipípedo (coseno de um ângulo)
• DIFICULDADE: *
• TEMPO MEDIO DE RESOLUCAO: 10 mn
• TEMPO MAXIMO DE RESOLUCAO: 20 mn
• PALAVRAS CHAVE: produto interno, norma, menor ângulo entre os vetores, coseno de um ângulo

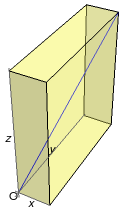
Considere o paralelipípedo de comprimento \(1\), largura \(4\) e altura \(4\).

O coseno do ângulo formado pela diagonal do paralelipipedo e o eixo dos xx é igual a:

A) \(\frac{4}{\sqrt{33}}\), B) \(3\sqrt{\frac{3}{11}}\), C) \(\sqrt{33}\), D) \(\frac{4}{33}\).

Para obter o zip que contém as instâncias deste exercício clique aqui[1]

Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt