Experiência de Thomson

Determinação experimental da relação $q/m$ do electrão

Objectivo do trabalho

Pretende-se com este trabalho determinar a relação entre a carga e a massa $q/m$ do electrão. Para esse fim, vamos estudar a deflexão de um feixe de raios catódicos sob o efeito de um campo eléctrico e de um campo magnético.

Conceitos fundamentais

Os raios catódicos foram descobertos em 1879 por William Crookes (1832--1919), mas foi Sir J. J. Thomson\footnote{Prémio Nobel da Física de 1906, em reconhecimento dos seus trabalhos teóricos e experimentais na condução da electricidade em gases.} (1856--1940) que, em 1897, relatou as experiências por si realizadas e que permitiram determinar o valor daquela relação. Além disso, estas experiências provaram que os raios catódicos são constituídos por partículas de carga negativa, desde então designadas por electrões. Neste trabalho iremos reproduzir aproximadamente a experiência de Thomson.

$$h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi$$

$${\mathbf E(r,z)} = E_0 \, \hat{\mathbf x} \, \frac{w_0}{w(z)} \exp \left( \frac{-r^2}{w(z)^2}\right ) \exp \left(\! -i \left(kz +k \frac{r^2}{2R(z)} - \psi(z) \right) \!\right)$$

Os raios catódicos foram descobertos em 1879 por William Crookes (1832--1919), mas foi Sir J. J. Thomson\footnote{Prémio Nobel da Física de 1906, em reconhecimento dos seus trabalhos teóricos e experimentais na condução da electricidade em gases.} (1856--1940) que, em 1897, relatou as experiências por si realizadas e que permitiram determinar o valor daquela relação. Além disso, estas experiências provaram que os raios catódicos são constituídos por partículas de carga negativa, desde então designadas por electrões. Neste trabalho iremos reproduzir aproximadamente a experiência de Thomson.

Campo electrostático

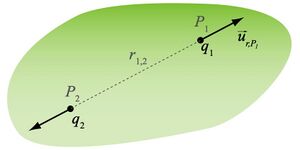
Define-se como sendo o campo eléctrico criado por uma distribuição de cargas que não evolui no tempo. Considere-se por exemplo o par de cargas $q_1$e $q_2$ imersas no vácuo, à distância $r_{12}$ e situadas respetivamente em $P_1$e $P_2$ conforme ilustrado na figura à direita. A força eléctrica que sofre $q_1$no ponto $P_1$devido a $q_2$em $P_2$à distância $r_{12}$é

Definição dos termos para a geometria de duas cargas

$$\begin{equation} \mathbf{F}_{P_1,q_1} (q_2, r_{1 2} ) =\frac{1}{4 \pi \varepsilon_0}\frac{q_1 q_2}{r_{1 2}^2} \hat{\mathbf{u}}_{r,P_1} = - \mathbf{F}_{P_2,q_2} (q_1, r_{1 2} ) \label{eq:eq1} \end{equation}$$

em que $\varepsilon_0$ é designada por constante dieléctrica ou permitividade eléctrica do vazio ($\varepsilon_0 \simeq 8.854 \cdot 10^{-12}$F/m) e $\hat{\mathbf{u}}_{r,P_1}$ é o versor da distância $r_{1 2}$ no ponto $P_1$ (vector unitário dirigido de $P_2$ para $P_1$, ver figura).

Dada uma carga $q_1$ e um ponto $P$ a uma distância $r$, define-se o campo eléctrico $\mathbf{E}$ em $P$como a força eléctrica por unidade de carga exercida sobre uma carga de prova ou teste, suposta unitária e positiva, colocada em $P$:

$$\mathbf{E}_P (q_1, r) = \frac{q_1}{4 \pi \varepsilon_0 r^2} \hat{\mathbf{u}}_{r, P}$$

As unidades do campo eléctrico são o newton/coulomb (N/C) ou, mais habitualmente, o volt/metro (V/m).

As linhas de força eléctrica geradas por $q_1$são radiais e dirigidas para o exterior, se $q_1>0$ ou para a origem, se $q_1<0$. Se se colocasse em $P$ a carga $q$, a força eléctrica a que esta carga ficaria submetida devido a $q_1$ seria $\mathbf{F}_{P,q} (q_1, r ) = q \mathbf{E}$ ou mais simplesmente:

$$\mathbf{F} = q \mathbf{E}$$

A expressão campo eléctrico também define a região do espaço onde se fazem sentir as acções eléctricas.

Potencial eléctrico

O campo eléctrico e a força eléctrica, que são entidades vectoriais, podem também ser calculadas a partir de uma função capaz de descrever o campo mas de natureza escalar, o potencial eléctrico $V$. Para a situação referida acima, o potencial eléctrico criado no ponto $P$ à distância $r$ da carga $q_1$ é calculado por:

$$\label{eq:pot_ele} V_P (q_1, r) = \frac{q_1}{4 \pi \varepsilon_0 r}$$

No caso de uma distribuição de $n$ cargas eléctricas $q_i$ à distância $r_i$ do ponto $P$ onde se pretende calcular o campo eléctrico e o potencial, tem-se para o campo eléctrico

$$\mathbf{E}_P = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^n \Big( \frac{q_i}{ r_i^2}\; \hat{\mathbf{u}}_{r_i , P} \Big)$$

e para o potencial

$$V_P = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^n \Big( \frac{q_i}{ r_i} \Big) \nonumber$$

Recorde-se que se se considera uma única carga $q_1$ positiva, as linhas de força eléctricas são radiais e dirigidas para o exterior. Essas linhas de força são perpendiculares às superfícies equipotenciais, que são esféricas $(r = \mathrm{c.^{te}})$ na equação $\ref{eq:pot_ele}$) e concêntricas com as cargas. Atendendo a ($\ref{eq:pot_ele}$) para dois raios $r_1$ e $r_2$ tal que $r_2 > r_1$ temos $V(r_2) < V(r_1)$ e portanto as linhas de força dirigem-se para os potenciais decrescentes.

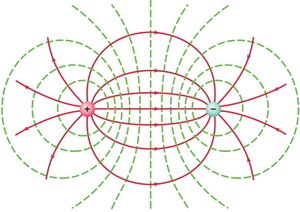
Considere-se agora o caso de duas cargas $q_1 > 0$ e $q_2 < 0$. Enquanto estiverem muito afastadas uma da outra, produzem campos radiais, respetivamente divergindo e convergindo. Se forem colocadas suficientemente próximas, as linhas de força vão sofrer a influência de ambas as cargas. Nesse caso, apenas uma única linha de força é linear, dirigida de $q_1$ para $q_2$. Todas as outras, que na vizinhança próxima de cada carga são radiais, acabam por infletir, dirigindo-se de $q_1$ para $q_2$. A figura das linhas de força tem simetria de revolução em torno do eixo que contém $q_1$ e $q_2$ e é esquematicamente a indicada na figura ao lado. Se o valor absoluto das duas cargas for o mesmo a figura é simétrica em relação ao plano mediatriz das cargas $q_1$ e $q_2$\footnote{Para mais exemplos ver https://phet.colorado.edu/en/simulations/charges-and-fields}.

Linhas de força (a vermelho) e superfícies equipotenciais (a verde) de duas cargas simétricas

Se se calcular a diferença de potencial entre dois pontos infinitamente próximos $P$ e $P+dP$ devida a uma carga $q_1$ à distância $r$ e $r+dr$ respetivamente, a variação elementar do potencial $V$ será:

$$d V = V_{P+dP} - V_P = \frac{q_1}{4 \pi \varepsilon_0 r} \big( \frac{1}{r + dr} -\frac{1}{r} \big) \approx \frac{q_1}{4 \pi \varepsilon_0 } \big( - \frac{dr}{r^2} \big) = - \mathbf{E} \cdot d \mathbf{r}$$

Esta quantidade representa o trabalho elementar (energia) associado ao deslocamento da carga teste ($q_t=1\,$C), de $P$ para $P+dP$. Para$q_1 > 0$ $\mathbf{E}$ e $\mathbf{dr}$ são paralelos e $dV < 0$. Isto significa que não será necessário fornecer energia para realizar esse transporte. De facto, afastar a carga teste da carga \(q_1$ (i.e. ir de $P$ para $P+dP$) leva a uma configuração de cargas $q_1$ e $q_t$ energeticamente mais favorável \footnote{Recorde-se que para um campo conservativo o trabalho realizado (que não depende do percurso mas só dos pontos inicial e final) tem um valor simétrico da variação de energia potencial.}.

No caso de uma diferença finita de potencial, isto é de uma diferença de potencial entre dois pontos $P$ e $Q$ ter-se-á que somar um número infinito de contribuições infinitesimais $dV_i=- \mathbf{E}_i \cdot d\mathbf{r}_i$ no intervalo de $P$ a $Q$:

$$V_Q-V_P = \lim_{n \to \infty } \sum_{i=1}^n dV_i = \lim_{n \to \infty } \sum_{i=1}^n \underbrace{( - \mathbf{E}_i \cdot d\mathbf{r}_i )}_{\overline{PQ}} \rightarrow \int - \mathbf{E} \cdot d\mathbf{r}$$

$$\begin{equation*} V_P - V_Q = \int_{\overline{PQ}} \mathbf{E} \cdot d \mathbf{r} \end{equation*}$$ e porque$\mathbf{E}$(campo electrostático) é um campo conservativo, este integral não vai depender do percurso mas apenas dos pontos extremos, i.e. $$\begin{equation*} V_P - V_Q = \int_P^Q \mathbf{E} \cdot d\mathbf{r} \end{equation*}$$

No caso particular de$E$ser homogéneo (por exemplo no interior de um condensador plano) na região onde se situam os pontos$P$e$Q$ afastados de uma distância$D$ obtém-se

$$\label{eq:difPot} V_P - V_Q = \mathbf{E}\cdot\mathbf{PQ}=E\cdot D$$

Para se compreender o significado físico de$V_P$ imagine-se que$Q$é um ponto infinitamente afastado da região em que se faz sentir o campo eléctrico$\mathbf{E}$. Nesse ponto,\(r \to \infty\( e\(V_Q=0$ obtendo-se$V_P = \int_P^\infty \mathbf{E} \cdot d\mathbf{r}$ que permite a seguinte interpretação: \newline \newline \fbox {

$$\begin{minipage}{36em} O potencial eléctrico\(V_P\)é a energia necessária para transportar a carga-teste, sob acção de\(\mathbf{E}\) desde o ponto\(P\)até uma distância suficientemente grande tal que o campo eléctrico não se faça sentir. \end{minipage}$$ } \newline \newline Assim,$V$tem sempre o significado de uma diferença de potencial.

%Se for a carga$q_2$ a energia necessária será\(W= q_2\cdot V$.

Energia electrostática

A energia associada a uma configuração de cargas$q_1$e$q_2$ à distância$r$ é dada por:

$$\label{eq:enrPot} W = \frac{q_1 q_2}{4 \pi \varepsilon_0 r} = q_1 V_1 = q_2 V_2 = \frac{q_1 V_1 +q_2 V_2}{2}$$ em que$V_1$é o potencial no ponto$P_1$criado pela carga$q_2$ e$V_2$é o potencial no ponto$P_2$criado pela carga\(q_1$.

Recordando a definição do potencial criado por$n$cargas eléctricas, podemos generalizar a equação ($\ref{eq:enrPot}$) na seguinte forma:

$$%\label{eq:enrPot} W_E = \frac{1}{2} \sum_{i,j (i\ne j)}^n \frac{ 1 }{4 \pi \varepsilon_0} \frac{ q_i \, q_j }{r_{i\,j}} = \frac{1}{2} \sum_{i=1}^n q_i \left( \sum_{j \ne i}^n \frac{ q_j }{4 \pi \varepsilon_0 \,r_{i\,j}} \right) = \frac{1}{2} \sum_{i=1}^n q_i V_i$$ que corresponde à energia necessária para criar a distribuição de cargas$q_i$. A energia\(W_E$é uma energia potencial porque está associada às posições que as diferentes cargas ocupam, podendo ser recuperada se as cargas se afastarem umas das outras até distâncias\(r \to \infty$.

Condutores eléctricos e dieléctricos. Condensador plano

Um material é um \emph{condutor eléctrico ideal} se as cargas eléctricas do mesmo sinal em excesso (que o carregam) são livres de se movimentarem no seu interior e à sua superfície. Quando pelo contrário isso não acontece, estamos perante um \emph{dieléctrico}.

Assim, se carregarmos um condutor com uma carga total$Q$(se$Q > 0$ significa que se retiram electrões ao condutor inicialmente neutro) essas cargas, todas do mesmo sinal, vão acomodar-se logo que se atinja o equilíbrio electrostático, em posições que são o mais afastadas possíveis umas das outras -- ou seja, na superfície exterior do condutor, formando uma ``folha de carga. Pode mostrar-se que$\mathbf{E}$no interior do condutor é nulo (enquanto que num dieléctrico\(\mathbf{E} \ne \mathbf{0}$), e que a superfície do condutor é uma \emph{equipotencial}: logo, as linhas de força eléctricas são-lhe perpendiculares. Quando um material é carregado, a velocidade com que essas cargas se transferem de todo o volume do condutor para a superfície depende da sua condutividade. Se se considerar um condutor carregado, com geometria plana (uma placa), a carga vai distribuir-se sobre a superfície (ver ilustração em baixo).

Ao colocar-se em frente uma placa idêntica, mas de carga simétrica, haverá uma redistribuição de carga que produz um campo eléctrico tal como ilustrado em baixo. Na região central, as linhas de força são paralelas entre si e o campo eléctrico é homogéneo. Nas extremidades as linhas de força emergem perpendicularmente à superfície mas encurvam, deixando de ser lineares. Esta geometria e distribuição de carga são características de um \emph{condensador plano}. A diferença de potencial entre as duas placas, afastadas de$D$ corresponde a ($V_+ \,–\, V_-) = E\cdot D\) pois$\mathbf{E}$é homogéneo (eq. $\ref{eq:difPot}$).\\

Pode mostrar-se que$\mathbf{E}$fica confinado à região entre as placas. Se o condensador fosse infinito (sem extremidades) teríamos três regiões, as duas exteriores ao condensador, onde o campo $\mathbf{E}$ é nulo, e entre as placas do condensador (também designadas por armaduras), onde o campo seria homogéneo.

Efeitos da corrente eléctrica estacionária criada por uma espira

A passagem da \emph{corrente eléctrica estacionária} (i.e. cuja intensidade não varia no tempo) por um condutor cria um campo magnético$\mathbf{B}$ além de produzir calor por efeito de Joule. As \emph{linhas de força magnética} produzidas por um fio condutor linear são circulares e concêntricas com o condutor (Fig. $\ref{fig:condutor}$). O módulo de$B$num ponto a uma distância$r$do fio (medida na perpendicular ao fio) é

$$|\mathbf{B_{\mathrm{fio}}}| = \frac{\mu_0 I}{2\, \pi \, r}$$

em que\(\mu_0 =  4 \pi× 10^{−7}\)H/m é a \emph{permeabilidade magnética}  do vazio. 

\begin{figure}[t]

\centering \includegraphics[width=0.5\textwidth]{fig-fio} \caption{Campo magnético produzido por um fio onde passa corrente.} \label{fig:condutor} \end{figure}

No caso de uma espira\footnote{Termo que designa um circuito eléctrico fechado} circular, é criado um campo magnético cujas linhas de força são curvas fora do seu eixo e lineares apenas ao longo do eixo (Fig. $\ref{fig:espira1}$). Pode provar-se que o campo magnético criado por uma espira de raio$r$ percorrida por uma corrente de intensidade$I$ tem linhas de força fechadas\footnote{Mesmo aquelas que só \emph{fecham} no infinito}, ao contrário das linhas de força eléctricas. Isto coloca em evidência que$\mathbf{B}$nos pontos do plano da espira, mas exteriores a esta, é antiparalelo a$\mathbf{B}$no eixo da espira (ver figura). O módulo de$\mathbf{B}$num ponto do eixo é dado por

$$|\mathbf{B}_{\mathrm{espira}}| = \frac{\mu_0 I}{2 r} \sin^3 \alpha$$

\begin{figure}[h]
 \centering 

\includegraphics[width=0.5\textwidth]{fig-espira.pdf} \caption{Campo magnético produzido por uma espira circular onde passa corrente.} \label{fig:espira1} \end{figure}

Força de Lorentz

Uma carga q animada de uma velocidade$\mathbf{v}$numa região em que existe um campo de indução$\mathbf{B}$e um campo eléctrico$\mathbf{E}$fica submetida a uma força de Lorentz\footnote{Se a força for apenas de origem magnética,$\mathbf{F}_m = q\,(\mathbf{v} \times \mathbf{B})$ pode chamar-se também de \emph{Laplace}}$\mathbf{F}$dada por:

$$\label{eq:Lorentz} \mathbf{F} = q\; \mathbf{E} + q\,(\mathbf{v} \times \mathbf{B})$$

A força de Lorentz resulta da soma vectorial de uma componente eléctrica e uma componente magnética, que verificam as seguintes propriedades:

$$\begin{itemize} \item a força eléctrica\(\mathbf{F_e}=q\mathbf{E}\)tem a mesma direção que o campo eléctrico; se a carga for positiva tem o mesmo sentido, se a carga for negativa tem o sentido oposto; \item a força magnética\(\mathbf{F_e}=q(\mathbf{v} \times \mathbf{B})\)é perpendicular ao plano definido pelos vectores velocidade\((\mathbf{v})\)e campo magnético\((\mathbf{B})\) sendo o seu sentido dado pela regra da mão direita para o produto externo de vectores. \end{itemize}$$ Quando a velocidade da carga e o campo magnético são mutuamente perpendiculares, a força magnética comporta-se como uma força centrípeta e a carga descreve uma trajectória circular (ver Fig. $\ref{fig:lorentz1}$) cujo raio se pode calcular igualando os módulos das duas forças\((|\mathbf{F_c}|=|\mathbf{F_m})|$:

\begin{figure}[t]

 \centering 

\includegraphics[width=0.4\textwidth]{./Lorentz1.png} \caption{Trajectória circular para uma carga positiva$q$com velocidade$\mathbf{v}$na presença de um campo magnético$\mathbf{B}_{in}$perpendicular. \label{fig:lorentz1}} \end{figure}

\begin{figure}[h]

 \centering 

\includegraphics[width=0.5\textwidth]{./Lorentz2.png} \caption{ Carga positiva$q$com velocidade$\mathbf{v}$ na presença de um campo magnético$\mathbf{B}_{in}$e um campo eléctrico\(\mathbf{E}$. Os três vectores são mutuamente perpendiculares e estão orientados de modo que as forças têm sentidos opostos. \label{fig:lorentz2}} \end{figure}

$$m\frac{v^2}{R}=qvB \rightarrow R=\frac{mv}{|q|B}$$

Um caso particularmente interessante da força de Lorentz verifica-se quando a velocidade da carga é perpendicular tanto ao campo eléctrico como ao magnético. Nesse caso, as duas forças têm a mesma direcção. Adotando uma configuração como a representada na Fig. $\ref{fig:lorentz2}$, as forças eléctrica e magnética têm sentidos opostos e podem compensar-se, anulando-se, o que permite que a carga mantenha uma trajectória rectilínea.

Nesta repetição da experiência de Thomson iremos utilizar estes dois princípios para determinar a razão\(q/m$. Num primeiro conjunto de medidas, iremos determinar o raio da trajectória de um feixe de raios catódicos na presença de um campo magnético. No segundo conjunto de medidas iremos equilibrar as forças de um campo magnético e um eléctrico de modo a que o feixe tenha uma forma aproximadamente rectilínea.

\newpage

Figuras dos aparelhos da montagem experimental

$$\begin{figure}[ht] \centering \includegraphics[width=0.45\textwidth]{./fig3-ThomsomEquip} \caption{Montagem da Experiência de Thomson com tubo de raios catódicos, suporte e par de bobinas de Helmholtz. \label{fig:Thomson_Equip}} \end{figure}$$

$$\begin{figure}[hb] \centering \includegraphics[width=0.4\textwidth]{./fig4-Thomson_Electron-Deflection-Tube-D} \caption{Trajectória dos electrões sujeitos a um campo magnético perpendicular. \label{fig:Thomson_trajec}} \end{figure}$$

\newpage

Procedimento Experimental

Material

1. Ampola (tubo) de raios catódicos (TRC), modelo TEL 525.
2. Fonte de alimentação do TRC, que inclui alimentação de alta tensão contínua (até 5000 V) aplicada aos eléctrodos (cátodo e ânodo) do TRC e alimentação de baixa tensão (6.3 V AC) para o filamento do TRC.
3. Par de bobinas que envolvem a parte esférica do TRC na configuração de Helmholtz (para criar um campo magnético aproximadamente homogéneo na região central entre as bobinas, de raio médio$r$ e afastadas de$r$uma da outra).
4. Fonte de alimentação de corrente \textbf{contínua} (em modo DC) para as bobinas.
5. Multímetro (como amperímetro) a instalar em \textbf{série} no circuito das bobinas.

O tubo TRC tem um filamento alimentado por 6.3 V (em modo AC). Este filamento emite electrões por efeito termiónico. Entre o ânodo e o cátodo do tubo estabelecem-se diferenças de potencial$(V_+ - V_-) = U_a$. Os electrões são acelerados entre o cátodo e o ânodo e a sua velocidade à saída do ânodo é função de\(U_a$.

Ao entrarem na parte esférica do tubo, os electrões podem ser deflectidos por \emph{campos magnéticos} provocados por correntes que percorrem as bobinas de Helmholtz e/ou por \emph{campos eléctricos} devidos à aplicação de tensão entre duas placas paralelas ligadas aos pontos 1 e 2 do diagrama (Fig. $\ref{fig:TL}$).

O campo de indução magnética$B$devido às bobinas de Helmholtz é aproximadamente uniforme na região central entre as bobinas, e para uma corrente$I$é dado por\footnote{No sistema SI, a unidade de campo magnético é o Tesla (T), sendo 1\,T=1\,Weber/m$^{2}\).}: \begin{align} \label{eq:helmotz} n &= 320\textrm{ espiras} \nonumber \\ B = \left(\frac{4}{5}\right)^{3/2} \cdot \frac{\mu_0 n I}{r} = \frac{32 \pi n }{5 \sqrt{5}} \cdot \frac{I}{r} \cdot 10^{-7}\textrm{ Weber/m}^{2}

\qquad  r  &= 0.068\textrm{ m} \\

r &= d/2 \nonumber \end{align}

$$\begin{figure} [h] \centering \includegraphics[width=1\textwidth]{fig5-TuboTL.pdf} \caption{Diagrama do tubo utilizado e geometria das bobinas de Helmholtz. Esquerda: vista lateral, com ligações eléctricas do filamento e da tensão de aceleração. Direita: vista frontal, com ligações das bobinas de Helmholtz. \label{fig:TL}} \end{figure}$$

Determinação de $q/m$ por deflexão magnética

Trajectórias de partículas carregadas sujeitas a um campo magnético constante

Quando se aplica uma tensão$U_a$entre o ânodo e o cátodo (sem aplicar tensão entre os pontos 1 e 2 representados na Fig. $\ref{fig:TL}$), pode admitir-se que a velocidade final$v$dos electrões ao abandonarem o ânodo é dada pela seguinte expressão

$$\label{eq:encin11} q\, U_a = \frac{1}{2} m \, v^2$$ em que$q$ é a carga do electrão e$m$a sua massa.

Os electrões entram, com velocidade horizontal, na parte esférica do tubo, onde são deflectidos pelo campo magnético$\vec{B}$(com$\vec{B}\perp\vec{v})$. A sua trajectória passa então a ser circular, com raio\(R$ verificando-se:

$$\label{eq:encin12} B \, q\, v = \frac{m\,v^2}{R}$$

As trajectórias dos electrões podem ser visualizadas numa escala graduada feita de material fluorescente. A origem do reticulado está situada aproximadamente no início da zona sujeita ao campo $\mathbf{B}$. Combinando ($\ref{eq:encin11}$) e ($\ref{eq:encin12}$) obtém-se uma expressão para a relação\(q/m$: \begin{equation} \label{eq:encin3}

\frac{q}{m} = \frac{2\, U_a}{B^2\,R^2} 

\end{equation} em que: \begin{description} \item[$U_a$] – impõe-se e mede-se diretamente no voltímetro da fonte de tensão. \item[$B$] – calcula-se, para uma dada corrente\(I\) a partir da expressão (\ref{eq:helmotz}). \item[$R$] – determina-se por leitura no écran fluorescente, das coordenadas de posição\(y\)(horizontal) e\(z\)(vertical) de pontos do feixe. Por construção do tubo verifica-se: \begin{equation} \label{eq:eR}

R = \frac{y^2 + z^2}{2 \, z} 

\end{equation} \end{description}

Modo de proceder

$$\begin{enumerate} \item Montar os circuitos eléctricos de acordo com a Fig. \ref{fig:TL}. Note que as ligações das bobinas devem garantir que a corrente eléctrica é percorrida no mesmo sentido, em ambas: para isso, deve usar os conectores na ordem\(A\rightarrow Z\)numa bobina e na ordem inversa na outra bobina. Chamar o docente para verificação, \textbf{antes de ligar os aparelhos}. \item Verfifique qual é o valor máximo da tensão disponível na fonte de alta tensão. Escolha um valor ligeiramente inferior. \item Ajustar a corrente das bobinas de Helmholtz\(I_+\)de modo a que a circunferência passe por um ponto bem determinado\footnote{Utilize de preferência os maiores valores possíveis para o raio\(R\) de forma a que o feixe se encontre na zona central entre as bobines.}. Calcule\(R$. Inverta o sentido da corrente e determine um novo\(I_-\)para o mesmo raio\(R$. Tomando\(I_{\textrm{medio}} = (I_+ + I_-)/2\( calcule o campo magnético\(B_{\textrm{medio}}$. Utilize a semi-diferença,\((I_+ - I_-)/2\) para a estimativa das incertezas\(\delta I_{\textrm{medio}}\)e\(\delta B_{\textrm{medio}}$. \item Repita o ponto 2) para quatro novos valores de\(R$. \item Repetir 1), 2) e 3) e para os mesmos\(R\) para dois valores inferiores de tensão, afastados por exemplo de 500 V entre si. \item Apresente os valores de\(q/m\)para os 15 pares de determinações. Calcule a média desses valores, assim como a incerteza da média. \item Para um dos pares de pontos, estime a contribuição relativa das incertezas das grandezas que mediu para a incerteza total. Compare este erro assim calculado com a incerteza calculada a partir dos 15 valores calculados. Apresente para cada raio o valor de\(q/m\)assim como o erro associado a cada uma das determinações. Compare e comente os resultados. \item Apresente um valor final para\(q/m$. Estime a precisão e a exatidão obtida nas determinações que realizou. \end{enumerate}$$

Determinação de $q/m$ por deflexão magnética e eléctrica quase compensada

Situação de equilíbrio entre as interacções eléctrica e magnética

Se, na força de Lorentz, os dois termos se equilibrarem -- ou seja, se as forças electrostática e magnética forem de igual módulo e de sentidos opostos -- a carga$q$não é desviada da sua trajectória. No nosso caso, em que$\vec{B} \perp \vec{v}$, a condição de equilíbrio é dada por: \begin{equation} \label{eq:equil1}

|\vec{E}| = v\, |\vec{B}|

\end{equation}

Montagem a efectuar

Aproveitando a montagem já efectuada no ponto anterior, ligue agora os terminais 1 e 2 (Fig. $\ref{fig:TLE}$) à fonte de alta tensão que gera a tensão$U_a$ produzindo assim na região do écran fluorescente um campo eléctrico. Fazendo com que as bobinas sejam percorridas por uma corrente com intensidade e ``sentido convenientes, podemos obter uma força de origem magnética anti-paralela à provocada pelo campo\(\vec{E}$. Deste modo, a trajectória visualizada no écran será aproximadamente retilínea, sendo a condição de equilíbrio dada por:

\begin{equation} \label{eq:equil2}

|\vec{E}| = v\, |\vec{B}| = \frac{U_a}{d}

\end{equation} onde$d$é a distância entre as placas do écran fluorescente e$U_a$a tensão entre as mesmas, que é como se disse igual à tensão de aceleração.

$$\begin{figure} [h] \centering \includegraphics[width=1\textwidth]{fig6-TuboTLE.pdf} \caption{Deflexão magnética e eléctrica quase compensada: ligações eléctricas do filamento, da tensão de aceleração e das placas. \label{fig:TLE}} \end{figure}$$

A equação ($\ref{eq:equil2}$) permite-nos calcular a velocidade dos electrões, uma vez que podemos conhecer os valores de todas as outras variáveis aí intervenientes. O conhecimento de$v$permite-nos calcular$q/m$tendo em conta que, segundo ($\ref{eq:encin11}$), deverá ser:

$$\begin{equation*} \label{eq:encin1} \frac{q}{m} = \frac{v^2}{2} \; \frac{1}{U_a} \end{equation*}$$

Ou finalmente, por combinação com ($\ref{eq:equil2}$):

$$\begin{equation} \label{eq:qmquase} \frac{q}{m} = \frac{1}{2} \; \frac{U_a}{B^2\; d^2} \end{equation}$$

Modo de proceder

$$\begin{enumerate} \item Para cada uma das quatro tensões de trabalho\(U_a\)já referidas, aplicadas agora também às placas que produzem o campo eléctrico, determine o valor de\(B\)(a partir de\(I$) que conduz ao anulamento das forças de origem eléctrica e magnética. \item Inverta o sentido dos campos eléctricos e magnéticos e repita a determinação do valor de\(B$. \item Apresente os valores de\(q/m$. Analise as diferentes contribuições para a incerteza total. Estime o valor da relação carga/massa do electrão, assim como a precisão e a exatidão obtida nas determinações que realizou. \item Observe a trajectória quando as forças de origem eléctrica e magnética não se compensam. Comente. % Apresente os valores de q/m calculados assim como o erro associado a cada determinação. Apresente um valor final para\(q/m$. \end{enumerate}$$