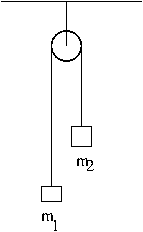
Máquina de Atwood com roldana

Metadata

• CONTEXTO : Primeiro ciclo universitário
• AREA: Física
• DISCIPLINA: Mecânica e ondas
• ANO: 1
• LINGUA: pt
• AUTOR: Ana Mourão
• MATERIA PRINCIPAL: Momento de Inércia
• DESCRICAO: Máquina de Atwood com roldana
• DIFICULDADE: ***
• TEMPO MEDIO DE RESOLUCAO: 1200 [s]
• TEMPO MAXIMO DE RESOLUCAO: 2400 [s]
• PALAVRAS CHAVE: Máquina, atwood, roldana, momento, inércia, rotação, corpo, rígido

Máquina de Atwood

Considere o sistema representado por uma roldana e duas massas. As duas massas \(m_1\) e \(m_2\) estão ligadas entre si por uma corda que passa pela roldana, como se vê na figura ao lado. A roldana pode ser aproximada por um disco de massa \(m_r=600\) g e raio \(R=2\) cm.

• Quais as expressões para a aceleração com que se deslocam as massas \(m_1\) e \(m_2\)? Compare com o resultado obtido para o caso com inércia da roldana desprezável.

 \marginpar{\includegraphics{\path/maquinadeatwood}}
   \ifthenelse{\not\boolean{SOL}}{%
   }{
   \minisec{Resolução:}
   Este problema é idêntico ao 3.6 já resolvido e parte da discussão aí feita 
   aplica-se a este caso. A diferença reside agora na consideração do papel
   da roldana. Com efeito ao rodar, a roldana tem momento angular. A acção 
   conjunta das duas forças $\vec{F}_i$ que se exercem em cada lado da roldana 
   (cada uma de módulo igual à tensão exercida pela corda na massa respectiva), 
   se não se equilibrarem, determinam a variação desse momento angular, isto é 
   uma aceleração angular, $\alpha$. \\
   \marginpar{
     \begin{tikzpicture}
     {
       \begin{scope}[black,line width=2pt,->] % P
         \draw (-1,-1.9) -- node[left=4pt] {\textit{$\vec{P}_1$}} (-1,-2.9);
         \draw (1,-1.4) -- (1,-2.2) node[below] {\textit{$\vec{P}_2$}};
       \end{scope}
       % Massas
       \begin{scope}[shape aspect=0.5, cylinder uses custom fill, cylinder end fill=red!50, cylinder body fill=red!25]
         \node[cylinder, rotate=90] at (-1,-1.5) {$m_1$};
         \node[cylinder, rotate=90] at (1,-1.0) {$m_2$};
       \end{scope}
       % Corda
       \draw[brown,line width=1.5pt] (-1,-1.0) -- (-1,1.5) arc[radius=1,start angle=180, end angle=0] -- (1,1.5) -- (1,0);
       \begin{scope}[green!70!black,line width=2pt,->] % F
         \draw (-1,1.5) -- node[left=4pt] {\textit{$\color{black}\vec{F_1}$}} (-1,0.5);
         \draw (1,1.5) -- node[right=4pt] {\textit{$\color{black}\vec{F_2}$}} (1,0.6);          
       \end{scope}
       % Roldana
       \draw[line width=0.5pt,->] (-0.84,2.4) arc[start angle=120, end angle=170, radius=.7] node[left=2pt] {\textit{$\color{black}\alpha$}};
       \fill[even odd rule, fill=orange!50] (0,1.5) circle (1); % (0,1.5) circle (0.7) (0,1.5) circle (0.15);
       \draw (0,1.5) -- node[below,] {\textit{$\color{black}R$}} (1,1.5);
       \draw[color=brown!80,line width=2pt] (0,1.5) -- (0,2.75);
       %
       \begin{scope}[red!70!black,line width=2pt,->] % T
         \draw (-1,-1) -- node[left=4pt] {\textit{$\color{black}\vec{T_1}$}} (-1,0);
         \draw (1,-0.5) -- node[right=4pt] {\textit{$\color{black}\vec{T_2}$}} (1,0.3);
       \end{scope}
     };
     \begin{scope}[on background layer]
       \fill[yellow!20] (-2.5,-3) rectangle (2,2.8);
     \end{scope}
     \end{tikzpicture}
   }
   Retomando as equações do problema 3.6 mas considerando agora que $T_1$ e $T_2$
   não são iguais ao contrário do que acontecia nesse problema, podemos escrever
   \begin{eqnarray}
     T_1 - m_1g &=& m_1 a_1 \label{R1} \\ 
     T_2 - m_2g &=& -m_2 a_1 \label{R2}
   \end{eqnarray}
   onde incluimos já o facto da aceleração de ambas as massas ter o mesmo módulo 
   mas sentidos opostos. Por outro lado, o efeito das forças $\vec{F}_i$ é
   \begin{equation}
    R F_1 - R F_2 = I\alpha \label{R3}
   \end{equation}
   onde $I$ é o momento de inércia. Se atendermos a que $\vec{F}_i = -\vec{T}_i$, 
   precisamos só relacionar a aceleração $a_1$ com a aceleração angular $\alpha$ 
   para podermos obter o valor de $a_1$. Para isso consideremos uma pequena 
   variação, $ds$, da corda na roldana quando esta gira de um ângulo $d\phi$. 
   Tem-se $ds = Rd\phi$, o que implica que $a_1 = R\alpha$.\\
   Subtraindo (\ref{R1}) de (\ref{R2}), usando (\ref{R3}) e as relações acima, 
   obtem-se
   \[ \frac{I}{R^2}a_1 + (m_1-m_2)g = - (m_1+m_2)a_1 \]
   usando o valor do momento de inércia para um disco em relação a um eixo central 
   encontrado no problema \ref{pb:disco} obtemos
   \[ a_1 = - \frac{m_1-m_2}{m_1+m_2+m_r/2}g\,, \quad a_2 = -a_1 \]
   Comparando com os resultados do problema 3.6 vemos que a aceleração é menor
   devido à massa da roldana e à variação do seu momento angular.\\
   \rule{\linewidth}{0.5pt}
   }    
 \item Qual a aceleração angular da roldana?
   \ifthenelse{\not\boolean{SOL}}{%
   }{
   \minisec{Resultado:}
   Da alínea anterior e da relação $a_1 = R\alpha$ vem
   \[\alpha = -{ m_1 - m_2 \over m_1 + m_2 +m_r/2}\frac{g}{R}\]
   \rule{\linewidth}{0.5pt}
   }  
   \item Qual a relação entre as massas para que o sistema esteja em equilíbrio?
   \ifthenelse{\not\boolean{SOL}}{%
   }{
   \minisec{Resultado:}
   As massas têm de ser iguais: $m_1=m_2$\\
   \rule{\linewidth}{0.5pt}
   }
 \item Considere $m_1 = \SI{200}{g}$ e $m_2 = \SI{100}{g}$. Calcule o valor
   das acelerações $a_1$ e $a_2$. Compare com a aceleração da gravidade.
   \ifthenelse{\not\boolean{SOL}}{%
   }{
   \minisec{Resultado:}
   Substituindo valores, obtemos:
   \[ a_1 = -\frac{1}{6}g\,, \quad a_2 = \frac{1}{6}g\]
   \rule{\linewidth}{2pt}
   }    
 \end{enumerate}

Respostas

\( (falta imagem) \)