Area de superfície de revolução

Metadata

• CONTEXTO : Primeiro ciclo universitário
• AREA: Matemática
• DISCIPLINA: Calculo diferencial e integral 2
• ANO: 1
• LINGUA: pt
• AUTOR: Equipa Calculo diferencial e integral 2
• MATERIA PRINCIPAL:
• DESCRICAO:
• DIFICULDADE: easy
• TEMPO MEDIO DE RESOLUCAO: 15 mn
• TEMPO MAXIMO DE RESOLUCAO: 30 mn
• PALAVRAS CHAVE:

Na figura abaixo está representada uma superfície de revolução, gerada pela função \(\text{y=}\frac{\text{sen}(z)}{2}\) com \(z \in [\)\(0\),\(\frac{\pi}{2}\)\( ]\), quando revolucionada em torno do eixo dos \(zz\).

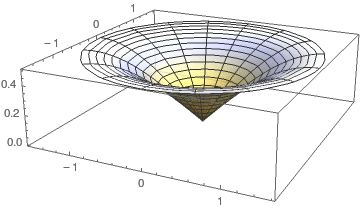A área da superfície de revolução é dada por:

A)\(\frac{\sqrt{5}\pi}{4}\)\(\pi\log\left(\frac{1}{2}+\frac{\sqrt{5}}{2}\right)\)

B)\(\frac{1}{8}\)\(\pi^2\)

C)\(\frac{\sqrt{5}}{8}\)\(\frac{1}{2}\log\left(\frac{1}{2}+\frac{\sqrt{5}}{2}\right)\)

D)\(3\sqrt{\frac{5}{2}}\pi\)\(\frac{1}{2}\pi\log\left(3+\sqrt{10}\right)\)

Para obter o zip que contém as instâncias deste exercício clique aqui(AreaSupRev)

Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt