Movimento Oscilatório

Fonte: My Solutions

Saltar para a navegação Saltar para a pesquisa

Metadata

Um pêndulo.

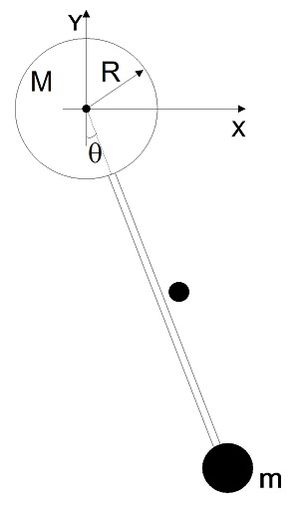
Considere o pêndulo representado na figura constituído por um disco de massa $M=1$ kg e raio $R=10$ cm, que roda livremente em torno do seu centro de massa e ao qual se encontra rigidamente fixado na periferia uma haste de massa desprezável. No outro extremo da haste encontra-se uma esfera de massa $m=0.2$ kg e dimensões desprezáveis. A distância entre o centro do disco e a massa m é $l=1$ m. O momento de inércia do disco em relação ao seu centro de massa é dado por $I_{CM} = \frac{1}{2} MR ^2$ .

Dados:

$g \simeq 10$ m.s $^{-2}$

Identifique os graus de liberdade e escreva o lagrangeano do sistema.

Respostas

O sistema tem um grau de liberdade descrito pela coordenada generalizada $\theta$ .

$L = \frac{1}{2} I \Big(\frac{d \theta}{dt} \Big)^2 + mgl\cos{\theta}$

com,

$I = \frac{1}{2}MR^2+ml^2$

Obtenha a(s) equação(ões) do movimento. Nota: Caso não consiga escrever o lagrangeano utilize qualquer outro método que saiba para chegar à(s) equação(ões) do movimento.

Respostas

$\frac{d^2\theta}{dt^2} + \frac{mgl}{I}\sin{\theta} = 0$

Para pequenas oscilações $\sin{\theta} \simeq \theta$

$\Rightarrow \frac{d^2\theta}{dt^2} + \frac{mgl}{I}\theta = 0$

Qual é a frequência própria do movimento na aproximação de pequenas oscilações?

Respostas

$\omega \simeq \sqrt{\frac{mgl}{I}} \simeq 3.12$ rad.s $^{-1}$

Sabendo que o pêndulo foi libertado de uma posição que faz 3º com a vertical sem velocidade inicial, determine a solução da equação de movimento.

Respostas

Para pequenas oscilações:

$\theta (t) = \frac{pi}{60}\cos{\omega t}$

$\simeq 0.0524 \cos{3.12 t}$ rad

Obtida de "http://www.mysolutions.tecnico.ulisboa.pt//wiki/index.php?title=Movimento_Oscilatório&oldid=331"